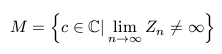
Yeditepe University
Information and Computer Science
Parallel MandelBrot Simulation
by PVM and OpenGL
Written by: Sadi Evren SEKER
Instructor: Esin Onbasioglu
1. Introduction:
In this report, analysis of Mandelbrot sets and computation of a simple Mandelbrot graph by using many computers will be discussed. There are many possibilities to compute a simple Mandelbrot graph by using parallel algorithms. This project covers 4 different calculation algorithm and their trade-offs.
Aim of this project is making a comparison between possible algorithms in parallel computing. We have selected Mandelbrot fractals as a mathematical target that can be computed in parallel. We have attacked this problem by using 4 different parallel algorithms and we have compared their work load for each process. In our terminology better algorithm means the better in distributing workload.
The Mandelbrot set is a set of complex numbers defined in the following way:
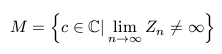
where:
![]()
That is, the Mandelbrot set is the set of all complex numbers which fulfill the condition described above, that is, if the value of the (recursive) function Zn for the value c is not infinite when n approaches infinity, then c belongs to the set.
As with many other fractal functions, it is said that this function has an attractor, which in this case is located at infinity.
Attractors are related to the "orbit" of the function. This orbit is defined by the path formed by the values of Z at each step n. The orbit of Z for a certain value c either tends towards the attractor or not. In this type of fractals a value c causing the orbit of Z to go to the attractor point is considered to be outside the set.
The attractor of a fractal may not always be at infinity, and there even may not be just one attractor. For example the so-called magnet1 fractal has two attractors, one at infinity and the other at 1+0i.

Figure 1(Graphical Diplay of Mandel-Brot Set)
Many people think that the Mandelbrot set is formed by the colors, or that they are part of it.
Actually the Mandelbrot set is that black shape in the middle. Everything that is outside that black shape is not a part of the set.
The Mandelbrot set is a set of complex numbers, so we graph it on the complex number plane. However, first we have to find many numbers that are part of the set. To do this we need a test that will determine if a given number is inside the set or outside the set. The test is based on the equation Z = Z2 + C. C represents a constant number, meaning that it does not change during the testing process. C is the number we are testing. Z starts out as zero, but it changes as we repeatedly iterate this equation. With each iteration we create a new Z that is equal to the old Z squared plus the constant C. So the number Z keeps changing throughout the test.
We're not really interested in the actual value of Z as it changes, we just look at its magnitude. The magnitude of a number is its distance from zero. For example, the number -9 is a distance of 9 from zero, so its magnitude is 9. The magnitude of a complex number is harder to measure. To calculate it, we add the square of the number's distance from the x-axis (the horizontal real axis) to the square of the number's distance from the y-axis (the imaginary vertical axis) and take the square root.
As we iterate our equation, Z changes and the magnitude of Z also changes. The magnitude of Z will do one of two things. It will either stay equal to or below 2 forever, or it will eventually surpass two. Once the magnitude of Z surpasses 2, it will increase forever. In the first case, where the magnitude of Z stays small, the number we are testing is part of the Mandelbrot set. If the magnitude of Z eventually surpasses 2, the number is not part of the Mandelbrot set.
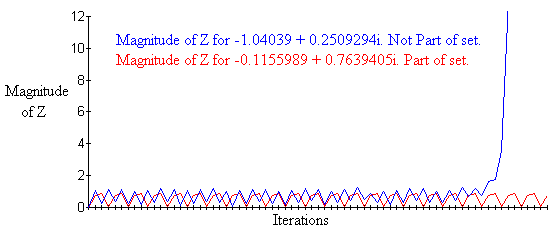
Figure 2 (Test of points in the MandelBrot Set)
As we test many complex numbers we can graph the ones that are part of the Mandelbrot set on the complex number plane. If we plot thousands of points, an image of the set will appear as on Figure 1.
2.3. Programming view of Mandel-Brot Sets
Consider a program that can compute the Mandelbrot set within a radius r of some complex points c1 and c2 with the answer (that is the number of iterations, less than lim, until divergence) displayed in screen by using an n by n array.
Please note that MandelBrot set is symmetric about the x-axis.
FOR I=1 TO 500
FOR J=1 TO 150
C1= -2+4*I/500
C2= 2-4*J/500
X=C1
Y=C2
FOR N=1 TO 50
X1=X*X-Y*Y+C1
Y1=2*X*Y+C2
R=X1*X1+Y1*Y1
IF R>4 THEN GOTO 1000
X=X1
Y=Y1
NEXT N
PSET(I,J)
PSET(I,500-J)
1000 NEXT J
NEXT I
END
It takes about half a second of real-time to call mandel as above. The execution time is quadratic with n.
3. PVM
PVM (Parallel Virtual Machine) is a software package that permits a heterogeneous collection of Linux and/or NT computers hooked together by a network to be used as a single large parallel computer. Thus large computational problems can be solved more cost effectively by using the aggregate power and memory of many computers. The software is very portable. The source, which is available free thru netlib, has been compiled on everything from laptops to CRAYs.
PVM enables users to exploit their existing computer hardware to solve much larger problems at minimal additional cost. Hundreds of sites around the world are using PVM to solve important scientific, industrial, and medical problems in addition to PVM's use as an educational tool to teach parallel programming. [2]
PVM forces us to use master/slaves based programming. There must be a master process to control all slaves and create an interface between user and the slave processes.
In this project we have used PVM version 3.
You can see installation details in appendix[howto install pvm on multiple computers]
4. What is OpenGL
OpenGL is a cross-platform standard for 3D rendering and 3D hardware acceleration. The software runtime library ships with all Windows, MacOS, Linux and Unix systems.
Today's applications and games manipulate massive amounts of data in real-time by using OpenGL hardware accelerated geometry, real-time lighting, clipping, transformations and rendering OpenGL delivers fast and complete 3D hardware acceleration.
It is possible to define OpenGL in many ways but by the view of this project OpenGL is used to print a calculated matrix to the screen.
As mentioned in PVM chapter, there must be a master process to create an interface for user. OpenGL must implemented in the master part for this interaction with user interface.
5. Parallel distribution of Mandelbort fractal
Any parallel algorithm uses divide and conquer algorithm to solve problems as shown on figure 3.
Any fractal in OpenGl is represented as a matrix. So we can divide this matrix to slaves. I did this division by using x-axis. For example I have used 500 x 500 matrix shown in the screen, each x pixel has 500 pixels in y-axis, and every "packet" is 1 x 500 vector.
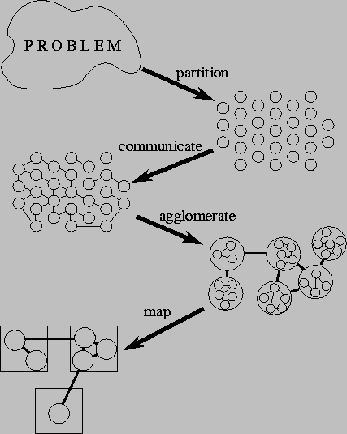
Figure 3(How to solve problem by parallel)
5.1. alg1
Simplest algorithm. Each packet is 1x500 vector. Calculation over x axis is done at master side and y axis in slave side. Each slave gets the column number (used to regenerate complete picture) and starts to calculate the relevant column.
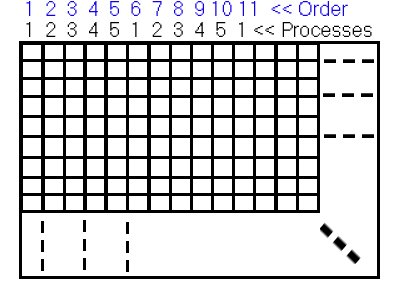
Figure 4(Matrix distribution by first algorithm)
Figure 4 shows the execution order and the distribution of matrix over processes. In the first step, slave 1 executes first column of matrix. Next step is execution of second column over second process. This goes on until every processes are executed 1 column. After the last process gets its column, every processes send their calculated data back to master (which yields a display operation on master) and master sends next available column (which is 6th in this case) to first finished process (which is also first available process).
There is not too much time difference in calculation of the columns since they are 1 x 500 array.
I have tried to run this algorithm over 4 computers by using pvm and average of my benchmarking results is 579000 miliseconds per run.
5.2. alg2
This algorithm is a little bit complicated than 5.1. In this case we send a 10 x 500 packet to slaves. Slaves calculate this range and send back to master the calculated array.
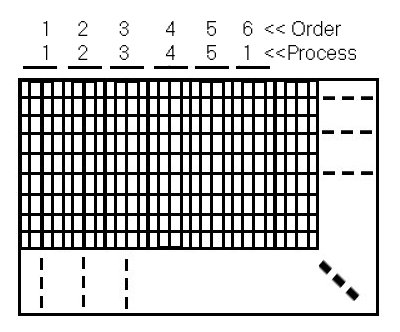
Figure 5 (Distribution of pixels over processors by using second algorithm)
Figure 5 shows the increase of packet size. Algorithm in 5.1. is implemented with different packet size. You should notice that in this new algorithm 2nd and 3rd columns are calculated on first process but in previous algorithm these columns were calculated on 2nd and 3rd slaves. So in this algorithm the difference between work load of each slave is higher than the previous algorithm.
I have run this algorithm over 4 computers parallel and average of my benchmarking results is 69000 miliseconds.
5.3. Jumping Algorithm
This case we have implemented an algorithm which master sends all slave 1 columns to slave1 with jumping other slave's columns. So slave1 gets all columns in a packet and calculates them at once.
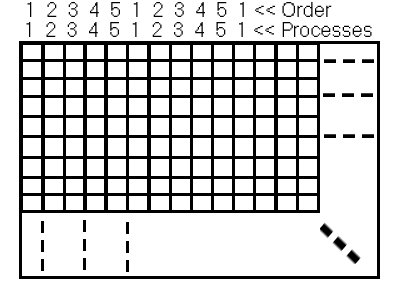
Figure 6 (Distribution of pixels over processors by Jumping Algorithm)
Above process numbers and the process numbers on figure 2 are same at all but the difference is the order. In the algorithm 5.1. calculation of matrix is done by a sequential order but here in this algorithm we have calculated by a jumping order. So after slave 1 has finished its job we do not need to turn back to slave1.
I have run this computer over 4 computers parallel and average of my benchmarking results is 513000 miliseconds.
5.4. Random
In this algorithm different than others, we have assigned slaves to random columns.
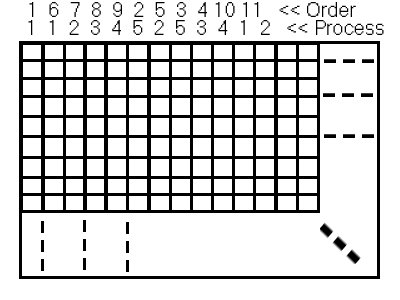
Figure 7(Distribution of pixels over processors by using random algorithm)
Above figure shows how randomly we have assigned slaves, columns and order. For this example orders of pixels are randomly distributed over processors.
Average running time of this algorithm over 4 parallel computers is about 503000 miliseconds.
6. Conclusion
This project shows that execution of a sequential and long problem can be easily reduced to a shorter execution time by using parallel algorithms. MandelBrot Set is an example to this long problem. It is also possible to find better or worse parallel algorithms than sequential. So making it parallel does not mean making it faster.
After implementation, execution and benchmarking it is obvious that using large number of packets increases computation time while decreasing network traffic. This decreases total calculation time.
9.Refrances
[1] www.opengl.org
[2] Linux PVM How-to,
[3] http://www.mhpcc.edu/training/workshop/parallel_develop/MAIN.html
[4] Chaos,Fractals, and Dynamics by Rober L. Devaney, Addison-Wesley Publising Co.
Environment: 4 Redhat Linux 7.1 over Dell pc
Software requirements: Pvm 3.4.3 and rsh 0.16 packages should be installed by rpm command.
System Settings: after installing rsh (Remote shell) there are some settings should be done to run on Linux machines.
put .rhosts files as below to users home directories (such as guest in this example)
localhost guest
pvm1 guest
pvm2 guest
pvm3 guest
pvm4 guest
set .bashrrc file as below to users home directories
PVM_ROOT=/usr/share/pvm3
export PVM_ROOT
switch to root and add all possible pvm hosts to /etc/hosts file (an example is shown below)
127.0.0.1 localhost.localdomain localhost
10.2.11.14 pvm1
10.2.11.15 pvm2
10.2.11.16 pvm3
10.2.11.17 pvm4
again as root add all hosts to /etc/hosts.equiv file as below
localhost
pvm1
pvm2
pvm3
pvm4
disable or set firewall with ipchains –F option (ipchains –L shows current status and if you want to make a tuning on firewall use appropriate options)
now setting all rsh options is completed you can check them by
rsh pvm2 echo ‘$PVM_ROOT’
if you can see /usr/share/pvm3 for all hosts than your remote shell setting is ok.
run pvm from command prompt and write add hostname to pvm console like below
add pvm1
add pvm2
add pvm3
add pvm4
you can see all hosts by typing conf in pvm console
Appendix [Code]
Sequential Algorithm
I.I. Master Side
#include</usr/share/pvm3/include/pvm3.h>
#include<GL/glut.h>
#include<iostream.h>
#include<malloc.h>
#include<assert.h>
#include <time.h>
#include <sys/time.h>
int xsize = 500, ysize = 500, ok=0;
double x1=-2.5, x2=1.5, y1=-2, y2=2, zx, zy, ***screen;
time_t tm;
struct timeval starttv, endtv;
struct timezone starttz, endtz;
float fark;
// PVM variables
const int TASKS = 10;
int tids[TASKS];
struct pvmhostinfo *hostp[TASKS];
float getdiff(struct timeval endtv, struct timeval starttv)
{
float diff=0;
diff=(endtv.tv_sec-starttv.tv_sec)*1000000+
(endtv.tv_usec-starttv.tv_usec);
return diff;
}
void init() {
glClearColor(0,0,0,0);
glShadeModel(GL_FLAT);
if (pvm_spawn("/pvm/proje2/alg1/slave", (char**)0, 0, "", TASKS, tids) < TASKS) {
cout << "Error spawning tasks - halt everything" << endl;
exit(1);
}
}
void display() {
if (ok) {
cout << "Displaying" << endl;
glBegin(GL_POINTS);
for(int x=0; x<xsize; x++)
for(int y=0; y<ysize; y++) {
glColor3f(screen[x][y][0], screen[x][y][1], screen[x][y][2]);
glVertex3f(x+0.5, y+0.5, 0);
}
glEnd();
}
else {
free(screen);
screen = (double***)calloc(xsize, sizeof(double**));
for (int i=0; i<xsize; i++) {
screen[i] = (double**)calloc(ysize, sizeof(double*));
for(int j=0; j<ysize; j++)
screen[i][j]= (double*)calloc(3, sizeof(double));
}
assert(screen);
glClear(GL_COLOR_BUFFER_BIT);
glLoadIdentity();
glBegin(GL_POINTS);
double a, b, ta, x ,y;
int it, max=-1, min=10000, maxit=int(1/(x2-x1)+1/(y2-y1)+20);
for(int i=0; i<xsize; i++)
for(int j=0; j<ysize; j++) {
x=x1+(x2-x1)*i/xsize;
y=y2-(y2-y1)*j/ysize;
it=0;
a=x; b=y;
while (it<maxit && a*a+b*b<4) {
ta=a*a-b*b+x;
b=2*a*b+y;
a=ta;
it++;
}
if (it>max) max=it;
if (it<min) min=it;
}
maxit=max;
for (int t=0; t<TASKS; t++) {
pvm_initsend(PvmDataDefault);
pvm_pkint(&t, 1, 1);
pvm_pkdouble(&y1, 1, 1);
pvm_pkdouble(&y2, 1, 1);
pvm_pkint(&ysize, 1, 1);
pvm_pkint(&max, 1, 1);
pvm_pkint(&min, 1, 1);
pvm_send(tids[t], 69);
}
int col, who, rcol;
for(col=0; col<TASKS; col++) {
x=x1+(x2-x1)*col/xsize;
pvm_initsend(PvmDataDefault);
pvm_pkint(&col, 1, 1);
pvm_pkdouble(&x, 1, 1);
pvm_send(tids[col], 666);
}
gettimeofday(&starttv, &starttz);
while (col<xsize) {
int rcol;
pvm_recv(-1, 254);
pvm_upkint(&who, 1, 1);
pvm_upkint(&rcol, 1, 1);
for(int i=0; i<ysize; i++)
pvm_upkdouble(screen[rcol][i], 3, 1);
x=x1+(x2-x1)*col/xsize;
pvm_initsend(PvmDataDefault);
pvm_pkint(&col, 1, 1);
pvm_pkdouble(&x, 1, 1);
pvm_send(tids[who], 666);
col++;
// display();
}
gettimeofday(&endtv, &endtz);
fark=getdiff(endtv, starttv);
ok=1;
glutPostRedisplay();
cout << "done" << endl << "time is :"<<fark;
}
}
void reshape(int w, int h) {
xsize=w; ysize=h;
glViewport(0, 0, GLsizei(w), GLsizei(h));
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
glOrtho(0, xsize, 0, ysize, -1, 1);
glMatrixMode(GL_MODELVIEW);
ok=0;
}
void showit(int x, int y) {
double a=x1+(x2-x1)*x/xsize, ia=a, b=y2-(y2-y1)*y/ysize, ib=b, ta;
int it=0;
glColor3f(1.0, 1.0, 1.0);
glBegin(GL_LINE_STRIP);
while (it<100 && a*a+b*b<4) {
glVertex3f(a, b, 0);
ta=a*a-b*b+ia;
b=2*a*b+ib;
a=ta;
it++;
}
glVertex3f(a, b, 0);
glEnd();
ok=0;
}
void main(int argc, char* argv[]) {
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);
glutInitWindowSize(xsize, ysize);
glutInitWindowPosition(100, 100);
glutCreateWindow("PVM Mandelbrot-o-Rama");
init();
glutDisplayFunc(display);
glutReshapeFunc(reshape);
glutMainLoop();
}
#include </usr/share/pvm3/include/pvm3.h>
#include <stdlib.h>
#include <fstream.h>
void main()
{
int mytid;
int min, max, ysize, col, master, it, who;
double y1, y2, x, y, a, b, ta;
// Initial information
pvm_recv(-1, 69);
pvm_upkint(&who, 1, 1);
pvm_upkdouble(&y1, 1, 1);
pvm_upkdouble(&y2, 1, 1);
pvm_upkint(&ysize, 1, 1);
pvm_upkint(&max, 1, 1);
pvm_upkint(&min, 1, 1);
master=pvm_parent();
mytid=pvm_mytid();
double** screen = (double **)malloc(sizeof(double *)*ysize);
for (int i = 0; i < ysize; i++)
screen[i]=(double*)malloc(sizeof(double)*3);
while (1) {
pvm_recv(-1, 666);
pvm_upkint(&col, 1, 1);
pvm_upkdouble(&x, 1, 1);
for(int j=0; j<ysize; j++) {
it=0;
y=y2-(y2-y1)*j/ysize;
a=x; b=y;
while (it<max && a*a+b*b<4) {
ta=a*a-b*b+x;
b=2*a*b+y;
a=ta;
it++;
}
if (it<max) {
screen[j][0]=double(it-min)/(max-min);
screen[j][1]=1-double(it-min)/(max-min);
screen[j][2]=double(it-min)/(max-min);
}
else screen[j][0]=screen[j][1]=screen[j][2]=0;
}
pvm_initsend(PvmDataDefault);
pvm_pkint(&who, 1, 1);
pvm_pkint(&col, 1, 1);
for(int i=0; i<ysize; i++)
pvm_pkdouble(screen[i], 3, 1);
pvm_send(master, 254);
}
}
Sequential Packet Algorithm
II.I. Master Side
#include</usr/share/pvm3/include/pvm3.h>
#include<GL/glut.h>
#include<iostream.h>
#include<malloc.h>
#include<assert.h>
int xsize = 500, ysize = 500, ok=0;
double x1=-2.5, x2=1.5, y1=-2, y2=2, zx, zy, ***screen;
// PVM variables
const int TASKS = 10;
int tids[TASKS];
struct pvmhostinfo *hostp[TASKS];
void init() {
glClearColor(0,0,0,0);
glShadeModel(GL_FLAT);
if (pvm_spawn("/pvm/proje2/alg2/slave", (char**)0, 0, "", TASKS, tids) < TASKS) {
cout << "Error spawning tasks - halt everything" << endl;
exit(1);
}
}
void display() {
if (ok) {
cout << "Displaying" << endl;
glBegin(GL_POINTS);
for(int x=0; x<xsize; x++)
for(int y=0; y<ysize; y++) {
glColor3f(screen[x][y][0], screen[x][y][1], screen[x][y][2]);
glVertex3f(x+0.5, y+0.5, 0);
}
glEnd();
}
else {
free(screen);
screen = (double***)calloc(xsize, sizeof(double**));
for (int i=0; i<xsize; i++) {
screen[i] = (double**)calloc(ysize, sizeof(double*));
for(int j=0; j<ysize; j++)
screen[i][j]= (double*)calloc(3, sizeof(double));
}
assert(screen);
glClear(GL_COLOR_BUFFER_BIT);
glLoadIdentity();
glBegin(GL_POINTS);
double a, b, ta, x ,y;
int it, max=-1, min=10000, maxit=int(1/(x2-x1)+1/(y2-y1)+20);
for(int i=0; i<xsize; i++)
for(int j=0; j<ysize; j++) {
x=x1+(x2-x1)*i/xsize;
y=y2-(y2-y1)*j/ysize;
it=0;
a=x; b=y;
while (it<maxit && a*a+b*b<4) {
ta=a*a-b*b+x;
b=2*a*b+y;
a=ta;
it++;
}
if (it>max) max=it;
if (it<min) min=it;
}
maxit=max;
for (int t=0; t<TASKS; t++) {
pvm_initsend(PvmDataDefault);
pvm_pkint(&t, 1, 1);
pvm_pkdouble(&y1, 1, 1);
pvm_pkdouble(&y2, 1, 1);
pvm_pkint(&ysize, 1, 1);
pvm_pkint(&max, 1, 1);
pvm_pkint(&min, 1, 1);
pvm_send(tids[t], 69);
}
int col, who, rcol;
for(col=0; col<TASKS; col++) {
x=x1+(x2-x1)*col/xsize;
pvm_initsend(PvmDataDefault);
pvm_pkint(&col, 1, 1);
pvm_pkdouble(&x, 1, 1);
pvm_send(tids[col], 666);
pvm_recv(-1, 254);
pvm_upkint(&who, 1, 1);
pvm_upkint(&rcol, 1, 1);
for(int i=0; i<ysize; i++)
pvm_upkdouble(screen[rcol][i], 3, 1);
}
ok=1;
//glutPostRedisplay();
display();
while (col<xsize) {
pvm_initsend(PvmDataDefault);
pvm_pkint(&col, 1, 1);
for(int l=0;l<10;l++){
x=x1+(x2-x1)*(col+l)/xsize;
pvm_pkdouble(&x, 1, 1);
}
pvm_send(tids[who], 666);
//finish send start receive
pvm_recv(-1, 254);
pvm_upkint(&who, 1, 1);
pvm_upkint(&rcol, 1, 1);
for(int l=0;l<10;l++)
for(int i=0; i<ysize; i++)
pvm_upkdouble(screen[rcol+l][i], 3, 1);
//kim oldugunu ogren ona gonder ogrenme burda gonderme loop
ok=1;
//glutPostRedisplay();
display();
col=col+10;
}
cout << "done" << endl;
}
}
void reshape(int w, int h) {
xsize=w; ysize=h;
glViewport(0, 0, GLsizei(w), GLsizei(h));
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
glOrtho(0, xsize, 0, ysize, -1, 1);
glMatrixMode(GL_MODELVIEW);
ok=0;
}
void showit(int x, int y) {
double a=x1+(x2-x1)*x/xsize, ia=a, b=y2-(y2-y1)*y/ysize, ib=b, ta;
int it=0;
glColor3f(1.0, 1.0, 1.0);
glBegin(GL_LINE_STRIP);
while (it<100 && a*a+b*b<4) {
glVertex3f(a, b, 0);
ta=a*a-b*b+ia;
b=2*a*b+ib;
a=ta;
it++;
}
glVertex3f(a, b, 0);
glEnd();
ok=0;
}
void main(int argc, char* argv[]) {
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);
glutInitWindowSize(xsize, ysize);
glutInitWindowPosition(100, 100);
glutCreateWindow("PVM Mandelbrot-o-Rama");
init();
glutDisplayFunc(display);
glutReshapeFunc(reshape);
glutMainLoop();
}
#include </usr/share/pvm3/include/pvm3.h>
#include <stdlib.h>
#include <fstream.h>
void main()
{
int mytid;
int min, max, ysize, col, master, it, who;
int lcol;
double y1, y2, x,lx[10],y, a, b, ta;
// Initial information
pvm_recv(-1, 69);
pvm_upkint(&who, 1, 1);
pvm_upkdouble(&y1, 1, 1);
pvm_upkdouble(&y2, 1, 1);
pvm_upkint(&ysize, 1, 1);
pvm_upkint(&max, 1, 1);
pvm_upkint(&min, 1, 1);
master=pvm_parent();
mytid=pvm_mytid();
double** screen = (double **)malloc(sizeof(double *)*ysize);
for (int i = 0; i < ysize; i++)
screen[i]=(double*)malloc(sizeof(double)*3);
double lscreen[500][10][3];
pvm_recv(-1, 666);
pvm_upkint(&col, 1, 1);
pvm_upkdouble(&x, 1, 1);
for(int j=0; j<ysize; j++) {
it=0;
y=y2-(y2-y1)*j/ysize;
a=x; b=y;
while (it<max && a*a+b*b<4) {
ta=a*a-b*b+x;
b=2*a*b+y;
a=ta;
it++;
}
if (it<max) {
screen[j][0]=double(it-min)/(max-min);
screen[j][1]=1-double(it-min)/(max-min);
screen[j][2]=double(it-min)/(max-min);
}
else screen[j][0]=screen[j][1]=screen[j][2]=0;
}
pvm_initsend(PvmDataDefault);
pvm_pkint(&who, 1, 1);
pvm_pkint(&col, 1, 1);
for(int i=0; i<ysize; i++)
pvm_pkdouble(screen[i], 3, 1);
pvm_send(master, 254);
while (1) {
pvm_recv(-1, 666);
pvm_upkint(&lcol, 1, 1);
for(int l=0;l<10;l++)
pvm_upkdouble(&lx[l], 1, 1);
for(int l=0;l<10;l++){
for(int j=0; j<ysize; j++) {
it=0;
y=y2-(y2-y1)*j/ysize;
a=lx[l]; b=y;
while (it<max && a*a+b*b<4) {
ta=a*a-b*b+lx[l];
b=2*a*b+y;
a=ta;
it++;
}
if (it<max) {
lscreen[j][l][0]=double(it-min)/(max-min);
lscreen[j][l][1]=1-double(it-min)/(max-min);
lscreen[j][l][2]=double(it-min)/(max-min);
}
else lscreen[j][l][0]=lscreen[j][l][1]=lscreen[j][2][2]=0;
}
}
pvm_initsend(PvmDataDefault);
pvm_pkint(&who, 1, 1);
pvm_pkint(&lcol, 1, 1);
for(int l=0;l<10;l++)
for(int i=0; i<ysize; i++)
pvm_pkdouble(lscreen[i][l], 3, 1);
pvm_send(master, 254);
}
}
Jumping Packet Algorithm
III.I Master Side
#include</usr/share/pvm3/include/pvm3.h>
#include<GL/glut.h>
#include<iostream.h>
#include<malloc.h>
#include<assert.h>
int xsize = 500, ysize = 500, ok=0;
double x1=-2.5, x2=1.5, y1=-2, y2=2, zx, zy, ***screen;
// PVM variables
const int TASKS = 10;
int tids[TASKS];
struct pvmhostinfo *hostp[TASKS];
void init() {
glClearColor(0,0,0,0);
glShadeModel(GL_FLAT);
if (pvm_spawn("/pvm/proje2/alg4/slave", (char**)0, 0, "", TASKS, tids) < TASKS) {
cout << "Error spawning tasks - halt everything" << endl;
exit(1);
}
}
void display() {
if (ok) {
cout << "Displaying" << endl;
glBegin(GL_POINTS);
for(int x=0; x<xsize; x++)
for(int y=0; y<ysize; y++) {
glColor3f(screen[x][y][0], screen[x][y][1], screen[x][y][2]);
glVertex3f(x+0.5, y+0.5, 0);
}
glEnd();
}
else {
free(screen);
screen = (double***)calloc(xsize, sizeof(double**));
for (int i=0; i<xsize; i++) {
screen[i] = (double**)calloc(ysize, sizeof(double*));
for(int j=0; j<ysize; j++)
screen[i][j]= (double*)calloc(3, sizeof(double));
}
assert(screen);
glClear(GL_COLOR_BUFFER_BIT);
glLoadIdentity();
glBegin(GL_POINTS);
double a, b, ta, x ,y;
int it, max=-1, min=10000, maxit=int(1/(x2-x1)+1/(y2-y1)+20);
for(int i=0; i<xsize; i++)
for(int j=0; j<ysize; j++) {
x=x1+(x2-x1)*i/xsize;
y=y2-(y2-y1)*j/ysize;
it=0;
a=x; b=y;
while (it<maxit && a*a+b*b<4) {
ta=a*a-b*b+x;
b=2*a*b+y;
a=ta;
it++;
}
if (it>max) max=it;
if (it<min) min=it;
}
maxit=max;
for (int t=0; t<TASKS; t++) {
pvm_initsend(PvmDataDefault);
pvm_pkint(&t, 1, 1);
pvm_pkdouble(&y1, 1, 1);
pvm_pkdouble(&y2, 1, 1);
pvm_pkint(&ysize, 1, 1);
pvm_pkint(&max, 1, 1);
pvm_pkint(&min, 1, 1);
pvm_send(tids[t], 69);
}
int col, who, rcol;
for(col=0; col<TASKS; col++) {
x=x1+(x2-x1)*col/xsize;
pvm_initsend(PvmDataDefault);
pvm_pkint(&col, 1, 1);
pvm_pkdouble(&x, 1, 1);
pvm_send(tids[col], 666);
pvm_recv(-1, 254);
pvm_upkint(&who, 1, 1);
pvm_upkint(&rcol, 1, 1);
for(int i=0; i<ysize; i++)
pvm_upkdouble(screen[rcol][i], 3, 1);
}
ok=1;
//glutPostRedisplay();
for(int k=0;k<10;k++){
pvm_initsend(PvmDataDefault);
pvm_pkint(&k, 1, 1);
for(int l=1;l<50;l++){
x=x1+(x2-x1)*(l*10+k)/xsize;
pvm_pkdouble(&x, 1, 1);
}
pvm_send(tids[who], 666);
//finish send start receive
pvm_recv(-1, 254);
pvm_upkint(&who, 1, 1);
pvm_upkint(&rcol, 1, 1);
for(int l=1;l<50;l++)
for(int i=0; i<ysize; i++)
pvm_upkdouble(screen[rcol+10*l][i], 3, 1);
//kim oldugunu ogren ona gonder ogrenme burda gonderme loop
ok=1;
//glutPostRedisplay();
display();
}
cout << "done" << endl;
}
}
void reshape(int w, int h) {
xsize=w; ysize=h;
glViewport(0, 0, GLsizei(w), GLsizei(h));
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
glOrtho(0, xsize, 0, ysize, -1, 1);
glMatrixMode(GL_MODELVIEW);
ok=0;
}
void showit(int x, int y) {
double a=x1+(x2-x1)*x/xsize, ia=a, b=y2-(y2-y1)*y/ysize, ib=b, ta;
int it=0;
glColor3f(1.0, 1.0, 1.0);
glBegin(GL_LINE_STRIP);
while (it<100 && a*a+b*b<4) {
glVertex3f(a, b, 0);
ta=a*a-b*b+ia;
b=2*a*b+ib;
a=ta;
it++;
}
glVertex3f(a, b, 0);
glEnd();
ok=0;
}
void main(int argc, char* argv[]) {
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);
glutInitWindowSize(xsize, ysize);
glutInitWindowPosition(100, 100);
glutCreateWindow("PVM Mandelbrot-o-Rama");
init();
glutDisplayFunc(display);
glutReshapeFunc(reshape);
glutMainLoop();
}
#include </usr/share/pvm3/include/pvm3.h>
#include <stdlib.h>
#include <fstream.h>
void main()
{
int mytid;
int min, max, ysize, col, master, it, who;
int lcol;
double y1, y2, x,lx[50],y, a, b, ta;
// Initial information
pvm_recv(-1, 69);
pvm_upkint(&who, 1, 1);
pvm_upkdouble(&y1, 1, 1);
pvm_upkdouble(&y2, 1, 1);
pvm_upkint(&ysize, 1, 1);
pvm_upkint(&max, 1, 1);
pvm_upkint(&min, 1, 1);
master=pvm_parent();
mytid=pvm_mytid();
double** screen = (double **)malloc(sizeof(double *)*ysize);
for (int i = 0; i < ysize; i++)
screen[i]=(double*)malloc(sizeof(double)*3);
double lscreen[500][50][3];
pvm_recv(-1, 666);
pvm_upkint(&col, 1, 1);
pvm_upkdouble(&x, 1, 1);
for(int j=0; j<ysize; j++) {
it=0;
y=y2-(y2-y1)*j/ysize;
a=x; b=y;
while (it<max && a*a+b*b<4) {
ta=a*a-b*b+x;
b=2*a*b+y;
a=ta;
it++;
}
if (it<max) {
screen[j][0]=double(it-min)/(max-min);
screen[j][1]=1-double(it-min)/(max-min);
screen[j][2]=double(it-min)/(max-min);
}
else screen[j][0]=screen[j][1]=screen[j][2]=0;
}
pvm_initsend(PvmDataDefault);
pvm_pkint(&who, 1, 1);
pvm_pkint(&col, 1, 1);
for(int i=0; i<ysize; i++)
pvm_pkdouble(screen[i], 3, 1);
pvm_send(master, 254);
while (1) {
pvm_recv(-1, 666);
pvm_upkint(&lcol, 1, 1);
for(int l=1;l<50;l++)
pvm_upkdouble(&lx[l], 1, 1);
for(int l=0;l<50;l++){
for(int j=0; j<ysize; j++) {
it=0;
y=y2-(y2-y1)*j/ysize;
a=lx[l]; b=y;
while (it<max && a*a+b*b<4) {
ta=a*a-b*b+lx[l];
b=2*a*b+y;
a=ta;
it++;
}
if (it<max) {
lscreen[j][l][0]=double(it-min)/(max-min);
lscreen[j][l][1]=1-double(it-min)/(max-min);
lscreen[j][l][2]=double(it-min)/(max-min);
}
else lscreen[j][l][0]=lscreen[j][l][1]=lscreen[j][2][2]=0;
}
}
pvm_initsend(PvmDataDefault);
pvm_pkint(&who, 1, 1);
pvm_pkint(&lcol, 1, 1);
for(int l=1;l<50;l++)
for(int i=0; i<ysize; i++)
pvm_pkdouble(lscreen[i][l], 3, 1);
pvm_send(master, 254);
}
}
IV. Random Algorithm
#include</usr/share/pvm3/include/pvm3.h>
#include<GL/glut.h>
#include<iostream.h>
#include<malloc.h>
#include<assert.h>
#include<stdlib.h>
#include<time.h>
int xsize = 500, ysize = 500, ok=0;
double x1=-2.5, x2=1.5, y1=-2, y2=2, zx, zy, ***screen;
// PVM variables
const int TASKS = 10;
int tids[TASKS];
struct pvmhostinfo *hostp[TASKS];
void init() {
glClearColor(0,0,0,0);
glShadeModel(GL_FLAT);
if (pvm_spawn("/pvm/proje2/alg1/slave", (char**)0, 0, "", TASKS, tids) < TASKS) {
cout << "Error spawning tasks - halt everything" << endl;
exit(1);
}
}
void display() {
if (ok) {
cout << "Displaying" << endl;
glBegin(GL_POINTS);
for(int x=0; x<xsize; x++)
for(int y=0; y<ysize; y++) {
glColor3f(screen[x][y][0], screen[x][y][1], screen[x][y][2]);
glVertex3f(x+0.5, y+0.5, 0);
}
glEnd();
}
else {
free(screen);
screen = (double***)calloc(xsize, sizeof(double**));
for (int i=0; i<xsize; i++) {
screen[i] = (double**)calloc(ysize, sizeof(double*));
for(int j=0; j<ysize; j++)
screen[i][j]= (double*)calloc(3, sizeof(double));
}
assert(screen);
glClear(GL_COLOR_BUFFER_BIT);
glLoadIdentity();
glBegin(GL_POINTS);
double a, b, ta, x ,y;
int it, max=-1, min=10000, maxit=int(1/(x2-x1)+1/(y2-y1)+20);
for(int i=0; i<xsize; i++)
for(int j=0; j<ysize; j++) {
x=x1+(x2-x1)*i/xsize;
y=y2-(y2-y1)*j/ysize;
it=0;
a=x; b=y;
while (it<maxit && a*a+b*b<4) {
ta=a*a-b*b+x;
b=2*a*b+y;
a=ta;
it++;
}
if (it>max) max=it;
if (it<min) min=it;
}
maxit=max;
for (int t=0; t<TASKS; t++) {
pvm_initsend(PvmDataDefault);
pvm_pkint(&t, 1, 1);
pvm_pkdouble(&y1, 1, 1);
pvm_pkdouble(&y2, 1, 1);
pvm_pkint(&ysize, 1, 1);
pvm_pkint(&max, 1, 1);
pvm_pkint(&min, 1, 1);
pvm_send(tids[t], 69);
}
int col, who, rcol;
for(col=0; col<TASKS; col++) {
x=x1+(x2-x1)*col/xsize;
pvm_initsend(PvmDataDefault);
pvm_pkint(&col, 1, 1);
pvm_pkdouble(&x, 1, 1);
pvm_send(tids[col], 666);
}
int l=col;
while (l<xsize) {
int rcol;
col=3*col%499;
pvm_recv(-1, 254);
pvm_upkint(&who, 1, 1);
pvm_upkint(&rcol, 1, 1);
for(int i=0; i<ysize; i++)
pvm_upkdouble(screen[rcol][i], 3, 1);
x=x1+(x2-x1)*col/xsize;
pvm_initsend(PvmDataDefault);
pvm_pkint(&col, 1, 1);
pvm_pkdouble(&x, 1, 1);
pvm_send(tids[who], 666);
l++;
ok=1;
display();
}
// glutPostRedisplay();
cout << "done" << endl;
}
}
void reshape(int w, int h) {
xsize=w; ysize=h;
glViewport(0, 0, GLsizei(w), GLsizei(h));
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
glOrtho(0, xsize, 0, ysize, -1, 1);
glMatrixMode(GL_MODELVIEW);
ok=0;
}
void showit(int x, int y) {
double a=x1+(x2-x1)*x/xsize, ia=a, b=y2-(y2-y1)*y/ysize, ib=b, ta;
int it=0;
glColor3f(1.0, 1.0, 1.0);
glBegin(GL_LINE_STRIP);
while (it<100 && a*a+b*b<4) {
glVertex3f(a, b, 0);
ta=a*a-b*b+ia;
b=2*a*b+ib;
a=ta;
it++;
}
glVertex3f(a, b, 0);
glEnd();
ok=0;
}
void main(int argc, char* argv[]) {
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);
glutInitWindowSize(xsize, ysize);
glutInitWindowPosition(100, 100);
glutCreateWindow("PVM Mandelbrot-o-Rama");
init();
glutDisplayFunc(display);
glutReshapeFunc(reshape);
glutMainLoop();
}
#include </usr/share/pvm3/include/pvm3.h>
#include <stdlib.h>
#include <fstream.h>
void main()
{
int mytid;
int min, max, ysize, col, master, it, who;
double y1, y2, x, y, a, b, ta;
// Initial information
pvm_recv(-1, 69);
pvm_upkint(&who, 1, 1);
pvm_upkdouble(&y1, 1, 1);
pvm_upkdouble(&y2, 1, 1);
pvm_upkint(&ysize, 1, 1);
pvm_upkint(&max, 1, 1);
pvm_upkint(&min, 1, 1);
master=pvm_parent();
mytid=pvm_mytid();
double** screen = (double **)malloc(sizeof(double *)*ysize);
for (int i = 0; i < ysize; i++)
screen[i]=(double*)malloc(sizeof(double)*3);
while (1) {
pvm_recv(-1, 666);
pvm_upkint(&col, 1, 1);
pvm_upkdouble(&x, 1, 1);
for(int j=0; j<ysize; j++) {
it=0;
y=y2-(y2-y1)*j/ysize;
a=x; b=y;
while (it<max && a*a+b*b<4) {
ta=a*a-b*b+x;
b=2*a*b+y;
a=ta;
it++;
}
if (it<max) {
screen[j][0]=double(it-min)/(max-min);
screen[j][1]=1-double(it-min)/(max-min);
screen[j][2]=double(it-min)/(max-min);
}
else screen[j][0]=screen[j][1]=screen[j][2]=0;
}
pvm_initsend(PvmDataDefault);
pvm_pkint(&who, 1, 1);
pvm_pkint(&col, 1, 1);
for(int i=0; i<ysize; i++)
pvm_pkdouble(screen[i], 3, 1);
pvm_send(master, 254);
}
}