Olasılığa Giriş ve Rasgele Süreçler

Yazan : Şadi Evren ŞEKER

Keywords: Stochastic Random Variable Rasgele değişken Rasgele süreçler Bayes Estimation Markov Chain Queueing Theory Random walks Decision Theory Model Kalman Filtering Wiever Filtering Monte Carlo

Sponsorlar:

Üniversitede Özel Ders SET Eğitim ve Danışmanlık

Stochastic Process ( Stokastik Süreçler veya Rasgele Süreçler) Tanımı :

1. Rasgele çıktı üreten bir seri olay veya süreç

2. Bir olasılık dağılımıyla tanımlanabilen süreçler

Olasılık Dağılımı: Olasılıkların olaylara nasıl dağıldığ.

Değişkenlik : Variability , Bir sistem veya olayın birini izleyen gözlemlerde tümüyle aynı sonuç üretmemesi.

Örnek: Arabanın yakıt / km verisi için arabanın durumu, kullanılan yakıt, hava durumu, trafik şartları vs. etkileri bulunmaktadır, bu etkilerden izole bir modelde arabanın kilometre başına harcadığı yakıt değişkendir.

Örneğin konnektör kalınlığının dirence etkisini ölçen bir mühendisin aşağıdaki konnektör direnç verilerini aldığını düşünelim:

X = m + e olarak hesaplanır. Burada m sabit değerken e rasgele bozunumdur.

Şeklindeki etkinin örnek kısmını konnektör, popülasyon kısmını ise müşteriye satılan bütün konnektörler oluşturmaktadır. Burada istatistiksel çıkarım kullanılmıştır.

Verilerin Toplanması:

Tarihsel yöntem : Geçmiş veriler incelenir

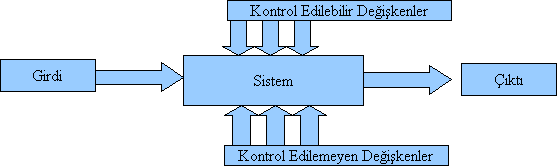
Gözlemsel : Hedefe yönelik deneyler tasarlanır

tasarlanmış olan denelerden bir kısmı sabit tutularak tekrarlanır ve bu yolla değişkenlerin sisteme etkileri ayrı ayrı incelenmiş olunur.

Örnek Uzay (Sample Space ) : Rasgele bir deneyin olan sonçlarının tamamının oluşturduğu küme.

S= R⁺ (örneğin konnektörün kalıklık uzayı)

S= { x | 10 < x < 11 } (kalınlığı 10 ile 11 arasında olan bir değişken)

S= { ince, orta, kalın } (3 ihtimalden birisi)

Örnek uzaylar, Discerete (ayrık) veya continous (sürekli) olabilirler.

2 adet konnektör olsaydı, örnek uzay S= R⁺ x R⁺ şeklinde gösterilecekti.

Event ( olay ) : Rastgele bir deneyin sonçlarının oluşturduğu örnek uzayın alt kümesidir.

De Morgan's Rule :

Permütasyon: S = { a, b, c} ise permütasyonu abc, acb, bac , bca , cab ,cba .... şeklinde olacaktır ve ihtimal sayısı P = n! Şeklinde hesaplanır.

Alt kümelerin permütasyonu : n elemanlı bir kümenin r elemanlı alt kümelerinin sayısı :

P_rⁿ = n x (n-1) x (n-2) ... (n-r+1) = n! / (n-r)! olarak hesaplanır.

Örneğin 8 boşluğa 4 eleman (her eleman birbirinden farklı) kaç farklı şekilde yerleştirilebilir.

P₄⁸ = 8! / 4! = 1680

Benzer nesnelerin permütasyonu: n = n1+n2+n3+ .... nr olduğuna göre

P = n! / n1!n2!n3!...nr! Olarak hesaplanır.

Örnek: Bir metal yüzeye 2 delik (aynı) ve 2 tane de diş (aynı) açılacak

n= n1+n2 ise 2+2= 4 ve olasılık da P = 4! / 2!x2! = 6 olur

Kombinasyon :Sıra önemsizdir,

olarak hesaplanır.

Örneğin 8 boşluğa 5 parça (aynı) için olasılık, = 56 olarak hesaplanır.

Rasgele Deney: Deneyin yapılmasından önce sonucu tahmin edilemeyen deneye denir.

Rasgele Değişken : Bir sagele deneyin herbir sonucuna karşılık gelen reel bir sayıdır.

Örneğin, örnek uzay s= { s1, s2, ... sn } olsun X(s) = x eşitliğini veren her değere rasgele değişken denir.

X'in uzayı reel sayıların bir kümesidir. { x : x= X(s= , s S)

Örneğin bir kafesten alınan farelerin cinsiyetine bakılan deneyde bu tanımlar aşağıdaki şekilde olur:

Örneğin Olayımız farenin sağlıklı olması olsun, buna göre : S= {D,E} , A= farenin sağlıklı olması. Buna göre çektiğimiz fare sağlılıysa olay oluşmuş olur. Yani deneyin belirli bir alt kümesi hedeflenmiş olur.

Zar örneğine bakılacak olursa, S= { 1, 2, 3, 4, 5, 6} olarak tanımlıdır ve olayımızı zarın tek gelmesi olarak alacak olursak, A= { 1, 3, 5} olarak tanımlamış oluruz. Bu durumda A , S'in bir alt kümesi olmuş olur. Örneğin zar atıldı ve 3 geldiyse olay olmuştur.

Örneğin, bir lotarya oyununda 3 haneli, rasgele bir sayı tutulacak buna göre S= {000,001,002, ... 999} olur ve örneğin tutulacak sayılar 121 211 ve 221 ise A={121, 211, 221} olarak verilmiş olur ve buna göre P(A) = 3/1000 olarak hesaplanır.

Bağıl frekans: İlk deneyde kafeste fare seçilince cinsiyeti tahmin edilemez, çünkü kafesteki farelerin oranı bilinmiyor dolayısıyla tahmin edilebilmesi için olayın müteaddit defalar tekrarlanması gerekir. Buna göre bağıl frekans formülü ile hesaplanır. Burada n büyüdükçe olasılık istikrarlı hale gelir.

Teori: Açıkça tanımlanmış aksiyomlardan mantık yolu ile geliştirilirler ve gerçek hayata uygulandığında işe yararlar.

Aksiyom: Doğruluğu kesin olarak kabul edilmiştir. Kendiliğinden aşikardır. Örneğin Bir şey hem var hem yok olamaz.

Olasılığın gerçek problemlere uygulanması:

1 Gözlem: Örneğin Hileli zar 1000 kere atılıyor ve 200 kere 5 geliyor. O halde 5 gelme olasılığı 2007 1000 dir. Eğer zar hileli değilse, 5 gelme olasılığı 1/6'dır.

2. Çıkarım: (Tümden gelim) Aksiyomlara dayalı olarak belirli olayların olasılığını çıkarmadır. Hileli olmayan zarda P(1) = P(2) = P(3) .. = P(6) = 1/6 olduğu bilinir.

3. Tahmin (kestirim) 1000 kere zar atıldığında kaç kere tek sayı geleceğinin tahmini ~500 dür.

Yukarıdaki 1. ve 3. adımlar tğme varım örnekleridir, 2. adım ise tümden gelimdir.

Olasılığın Tanımı : Olasılığın tanımına dair 3 ayrı yaklaşım bulunmaktadır. Bunlar Aksiyometrik tanım, Bağıl Frekans Tanımı ve Klasik Tanımdır. Bunların açıklamaları aşağıda verilmiştir:

Aksiyometric tanım 3 varsayıma dayanmaktadır bunlar:

1. P(S) = 1 , yani kesin olayın olasılığının 1 olması

2. 0 <= P(A) <= 1 yani bir A olayının pozitif bir sayı alması

3. A ile B mutually exclusive ise olarak hesaplanır.

Basit frekans tanımı: (n sonsuza giderken olasılık istikrarlı hale gelip skalar sayı ile bulunabilir) bu hipotez, gözlem ve tahmin adımlarında kullanılabilir.

Klasik Tanım: olarak hesaplanır ve burada N olası sonuçların sayısı, NA ise A olayının olası sonuçlarının sayısıdır. Gerçek deneyden önce bu yöntemle olasılık kestirilebilir. Örneğin Zarın tek gelmesi S= {1,2,..,6} , N=6 , NA=3 olur ve P(A) = 3/6 olarak önceden hesaplanabilir.

Klasik tanımın hatalı olabileceği durumlar:

Örneğin 2 kere zar atılıyor. A olayı, 2 zarın toplam 7 gelme olasılığı olsun. Klasik tanımda P(A) nasıl hesaplanır?

1. çözüm : S, zarların toplamları olsun yani S= {2,3,4,..12}, bu durumda N = 11 ve NA= 1 olduğuna göre P(A) = 1/11 olarak hesaplanır ancak yanlıştır.

2. Çözüm: S, zarların ikili olasılıkları olsun, yani S= {(1,1),(1,2),(1,3)...(6,6)} (burada 1,2 ile 2,1 aynı kabul edilmiştir) buna göre :N= 21 olur ve A={(3,4),(5,2),(6,1)} olduğuna göre NA=3 olur. Sonuç olasılığı P(A) = 3/21 olarak hesaplannır ancak bu sonuç da yanlıştır.

3. Çözüm: zarların 1 ve 2. zar olarak ayrılması S= {(1,1),(1,2),(2,1)...(6,6)}(burada 2. çözümden farklı olarak, zarlar ayrı kümelerde incelenmiş ve 1,2 ile 2,1 farklı olaylar olarak ele alınmıştır), buna göre N= 36 bulunur ve A= {(3,4),(5,2),(6,1),(4,3),(2,5),(1,6)}, ve P(A)= 6/36 = 1/6 olarak hesaplanır ve bu doğru sonuçtur.

Dolayısıyla Klasik tanımda değişikliğe gidilmiş ve “Bir olayın, olasılığı bütün olası sonuçların eşit olması koşuluyla sınırlandırılmıştır” buna göre yukarıdaki zar örneğinde,

1. çözümde toplam 2 gelmesi olasılığı (1,1) ike 4 gelmesi olasılığı (2,2) (3,1) (1,3) olmaktadır, buna göre 2 gelmen durum sayısı 1 iken 4 gelen durum sayısı 3 olmaktadır, ancak S kümesine 1'er eleman gibi yerleştirilmişlerdir, bu durumda olasılıkları eşit kabul edilmiştir oysaki eşit değildirler.

2. Çözümde (1,1) gelmesi ihtimali ancak iki zarında 1 gelmesi durumunda olurken (1,2) gelmesi 1. zarın 1 gelmesi ve 2. zarın 2 gelmesinde olabileceği gibi 1. zarın 2 gelmesi ve 2. zarında 1 gelmesi durumunda da olabilir, oysaki bu iki ayrı ihtimal S kümesinde tek bir ihtimal gibi yer almış ve (1,2) ihtimaliyle (1,1) ihtimaline aynı oran verilmiştir, oysaki değildir.

3. Çözümde bütün ihtimaller ortak oranlarda yer almış ve sonuç doğru çıkmıştır.

Örnek: Yeni doğan bebeğin cinsiyetinin tahmini. Kız / Erkek olabilir. Ancak ½ denilemez, olay, ailesinin geçmişi, bölgesel şartlara vs. bağlı olabilir.

Klasik yöntem için sıkıntılı olan bir diğer durum ise, sonsuz olasılık durumudur. (bkz. Mere Paradoxu)

Koşullu Olasılık (Conditional Probability):

Rasgele deneyimiz sadece B alt kümesinin elamanı olan sonuçlar ile ilgiliniyoruz. Burada S örnek uzay, B ise örnek uzayın bir alt kümesidir. Verilen tüm A olayı P(A|B) şeklinde gösterilir.

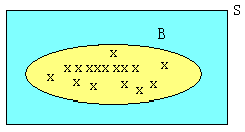
, P(B) > 0 (verilen A olayının, B olmuşsa olma olasılığı)

Örnek, 20 tane lale soğanı arasından, 8 tanesi erken, 12 tanesi geç açacak ve 13 tanesi kırmızı ve 7 tanesi sarı olacak. Bu durumda ilave bilgilerle aşağıdaki tablo çıkarılabilir:

Erken açacak lale soğanları göz önüne alınırsa 8 sayısı bulunur. Bu soğanların ayrıca krımızı olması da isteniyorsa P(K|E) ihtimali modellenmiş olur, bu ihtimalin sayısal değeri ise 5/8 olur.

Bağımsız olaylar (Independent events) : Bazı olay çiftleri için birinin olması diğerinin olmasını değiştirirse bu iki olay bağımsız olaylardır, değiştirirse bağımlı olaylardır.

A ve B olayları sadece ve sadece

A ve B bağımsız ise A' ve B' de , A' ve B de, A ve B' de birbirinden bağımsızdır.

A,B,C olaylarının birbirinden bağımsız olması için olması gerekir.

Örnek: Bir kutuda, 1,2,3,4 olarak numaralandırılmış 4 top var. 1 top, rastgele seçiliyor A= {1,2} , B={1,3}, C={1,4} olsun. P(A)=P(B)=P(C)=1/2 olur.

ve dolayısıyla bağımsızlık koşulunu sağlarlar. Ancak

dolayısıyla A,B,C olayları bağımlı olaylardır.

Örnek:

Bir bozuk paranın 2 kere atılması sonucunda 3 olay tanımlansın. Bunlardan A, ikinci atışta yazı gelme olasılığı, B, ilk atışta tura gelme olasılığı ve C, hep yazı gelme olasılığı olsun. Bu olayların bağımlı mı, bağımsız mı olduğunu bulalım.

Örnek uzayımız S = {TT, TY, YT, YY} olarak tanımlanır. Olaylar sırasıyla:

A = {TY, YY}

B = {TY, TT}

C = {YY} olurlar.

Yukarıdaki olaylarda A olayının olma olasılığı 2/4 = ½ dir (örnek uzayda kapladığı alan)

C olayının olmasından sonra A olayının olma olasılığı P(A|C) = 1 dir. Çünkü A olayı C olayını kapsar.

B olayının olmasından sonra A olayının olma olasılığı ise

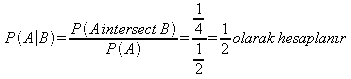
Dikkat edilirse B olayından sonra A olayının ilk olasılık değeri olan ½ değişmemiştir, dolayısıyla B ile A olayları bağımsız olayladır. Ancak C olayından sonra ilk değeri ½ olan A olayının olasılık değeri 1 olmuş ve C olayından etkilenmiştir. Bu durumda A ile C olayları bağımlı olayladır denilebilir.

Çarpım kuralı:

Toplam olasılık kuralı: S kümesinin n tane alt kümesi olması durumunda,

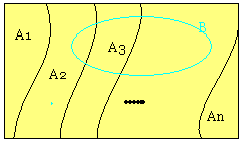
Partition U = [A1,A2,...An] olur. Burada U , S'in bir bölümlendirmesi olmak üzere , B'de rasgele seçilmiş bir olaysa P(B) = P(B|A1).P(A1)+P(B|A2).P(A2)...+P(B|An).P(An) olur.

Ispatı: Ai, Aj mutually exclusive iki olay olsun. BAi ve BAj karşılıklı birbirini dışlayan olaylardır. P(BS)=P(BA1).P(BA2)...P(BAn)

Örnek:

iki kişi sırasıyla zar atıyorlar, büyük zar atan kazanıyor. 1 kişinin 10 kere üst üste kazanma ihtimali nedir?

1. kişinin attığı zar analiz edilirse toplam kuralına uygun bir şekilde soru çözülebilir. Buna göre:

1 atarsa P(B) = 0 dır. Çünkü kazanamaz.

2 atarsa P(B) = 1/6 * 1/6 = 1/36 dır. (2. kişinin 1 atması durumunda (1/6 ihtimalle) kazanır, 2 atması ihtimali de 1/6 dır)

3 atarsa P(B) = 1/6 * 2/6 = 2/36

...

6 atarsa P(B) = 1/6 * 5/6 = 5/36 olarak hesaplanır.

Toplam kuralı uygulanırsa 1/36 + 2/36 + ... + 5/36 = 5/12 olarak bulunur.

Soruda 10 kere üst üste kazanma ihtimali istendiği için sonuç

Koşullu olasılık tanımı halini alır dolayısıyla P(BAi) = P(B|Ai).P(Ai) olur.

P(B)= P(B|A1).P(A1)+ ... + P(B|An).P(An) olur.

Bayes Teoremi : bu eşitlik bayes theorem'idir.

Örnek Yay üreten 3 Makine için aşağıdaki hata ve üretim oranları veriliyor:

Üretilen yaylardan rasgele birisi seçildiğinde bozuk olma olasılığı: P(B)=P(I)P(B|I)+P(II)P(B|II)+P(III)P(B|III),

olarak hesaplanır.

Eğer yay bozuk çıktıysa bunun 3. makineden çıkma olasılığı aşağıdaki şekilde hesaplanır:

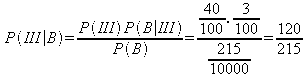
Örnek:

Bütün nufusta yapılan bir hastalık testinde (+) pozitif sonucun doğru bilinme olasılığı 0.99 ve (-) negatif sonucun doğru bilinme olasılığı 0.95 olarak veriliyor. Hastalığın bütün nufusta görülme olasılığı ise 0.0001 ise test sonucu pozitif çıkan bir kişinin hasta olma olasılığı nedir?

D olayı kişinin hasta olma olasılığı olsun

D' olayı kişinin hasta olmama olasılığını göstermiş olur.

Buna göre P(D) = 0.0001 olur

S olayı ise testin (+) çıkma olasılığı olsun.

S' olayı testin (-) çıkma olasılığını göstermiş olur.

Buna göre P(S'|D') = 0.95 olduğuna göre P(S|D') = 0.05 olur.

Soruda istenen durum P(D|S) ile gösterilebilir ve şartlı ihtimal hesabından

ancak burada Dolayısıyla bayes teoremini uygulamayı deneyebiliriz. Buna göre

olarak bulunur. S olayı için iki ihtimal bulunduğundan ( test sonucu ya (+) ya da (-) çıkabilir) olasılık modeli aşağıdaki şekilde olur:

olur. Sonuç ise olarak bulunur.

Ayrık Tip Dağılımlar (discrete Distribution )

Ragelen değişken: Rasgele deneyin her bir sonucuna reel bir değer atayan bir fonksiyondur.

s, S örnek uzayınının bir elemanıdır.

X(s) = x,

X'in uzayı, = {} olarak gösterilir.

R uzayı, sonlu sayıdaki pozitif tam sayılardan oluşmuşsa R ayrık bir örnektir. X de ayrık tipte rasgele değişken olmuş olur.

Olasılık Yoğunluk Fonksiyonu (Probability Dense Function PDF)

P(X=x) = f(x) olarak gösterilir. Özellikleri:

a f(x) > 0 ,

b

c P(x = A) =

Örnek:

1 derse 50 öğrenci devam ediyor bu öğrencilerde 11 kişi 1. sınıf, 19 kişi 2. sınıf, 14 kişi 3. sınıf ve 6 kişi 4. sınıftan. Rasgele öğrenci seçiliyor, yoğunluk dağılım fonksiyonunu bulunuz.

X'in alabileceği değerler X= 1,2,3,4 olur ve x'in olasılık yoğunluk fonksiyonu:

f(1) = P(x=1) = 11/50

f(2) = P(x=2) = 19/50

f(3) = P(x=3) = 14/50

f(4) = P(x=4) = 6/50

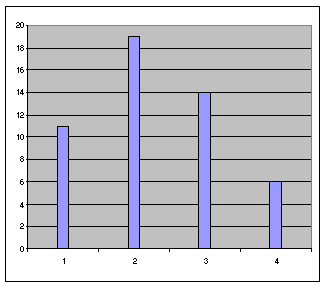
olasılık yoğunluk fonksiyonunun çizgi grafik ile gösteirmi yukarıdaki şekildedir.

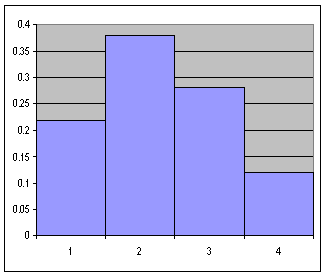
Olasılık yoğunluk fonksiyonunun histogram grafiği ise yukarıda gösterildiği şekildedir.

Kümülatif Dağılım Fonksiyonu (cumulative distribution function cdf)

dağılım fnonksiyonlarında X=x için f(x) = P(X=x) olarak tanımlanmıştı, kümülatif değeri ise

X<= x yani f(x) = P(X<=x) olan fonksiyondur ve F(x) olarak gösterilir.

Örneğin X=1,2,3 için F(x) = X/6 olarak tanımlı olsun. Buna göre

P(X<=1) = f(1) = 1/6

P(X<=2) = f(1) + F(2) = 1/6 + 2/6 = ½ olacaktır dağılım grafikleri ise aşağıda verilmiştir.

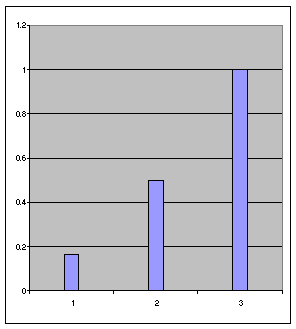
Ayrıca p(x <= 3/2) değerinin de tanımlı olduğunu ve bu değer için de 1/6 sonucunu alacağımızı düşünürsek aşağıdaki grafik de doğru olur:

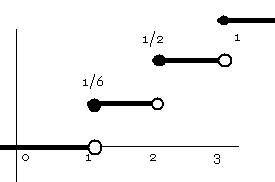
Örnek :

4 yüzlü zar 2 defa atılıyor.

X iki sonucun toplamı olur.

X'in alabileceği değerler 2,3,..8

X'in olasılık yoğunluk fonksiyonu olarak verilmiş olsun. Ve zar 1000 kere atılıyor olsun

Örnek olarak f(2) = 1/16 + f(3) = 2/16 ... f(8) = 1/16 bulunur.

Nümerik Beklendik Değer (Numerical Expected Value)

P, tek deneydeki başarı sayısı olsun.

k, deneylerin tekrar sayısı olsun

k deney için beklenen nümerik başarı sayısı : pk olarak hesaplanır

Matematiksel Beklenilen Değer (Mathematical Expected Value)

Ortaya konulan bir ödül için belirli bir başarı oranıyla, olayın beklenen maliyetini hesaplamada kullanılır.

Örneğin

a ödül miktarı için

p başarı ihtimaliyle

E = a.p olarak hesaplanır.

Örnek:

500 biletlik bir çekilişte, 325 ytl ödül bulunsun, bilet parasının beklenen değeri nedir?

E = 325 x 1/500 = 0.65ytl maliyet değerine sahiptir.

Matematiksel beklendik değer ,

benzer şekilde u(x) fonksiyonu için

Örnek:

Bir zar oyununda, 1,2,3 sayıları gelmesi durumunda oyuncu 1 ytl, 4 veya 5 gelmesi durumunda 5ytl ve 6 gelmesi durumunda 35 ytl ödül kazanıyor. Buna göre zar atmanın maliyeti oyuncu için kaç ytl'dir?

A= {1,2,3} -> 1ytl

B= {4,5} -> 5ytl

C= {6} -> 35ytl

E[u(x)] = 3/6 + 5.2/6 + 35. 1/6 = 8ytl olarak hesaplanır.

u(x) de kendi başına bir rasgele değişkendir. Bu rasgele değişkene Y diyelim ve Y'nin olasılık yoğunluk fonksiyonu g(Y) olsun. Buna göre

E(Y) = olur

Beklenen değer hesaplamada kolaylık sağlayacak bağlantılar:

E[c] = c (sabit değer için)

E[c u(x)] = c E[u(x)]

Varyans

Ortalamanın yayılmasının ölçülmesidir.

Standart Sapma

Bernoulli Denemeleri ve Binom Dağılımı

Örneğin yazı – tura deneyinde : X rasgele değişken, ve tura başarı olsun.

x(y) = 0 , q ve x(t) = 1 , q olarak kabul edilirse

p{ x = 1 } = p ve p { x = 0 } = q = 1 – p olarak yazılabilir

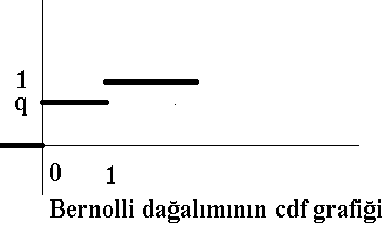
X, başarılı ve başarısız değerlerini alıyorsa Bernolli dağalımına sahip denilir.

P, denemeden denemeye sabit kalana kadar deney tekrar edilir ve donuçta “Bernoulli denemeleri dizisi” oluyor.

Örnek: Bir kutuda 10 kırmızı , 20 beyaz top var. Kutuya geri konarak, her seferinde 1 top olmak üzere 5 top çekiliyor.

Bu örnekte yerine konularak çekildiği için, bağımsız olaylar incelenmiştir. 5 top çekilmesi işlemi, 5 bernoulli denemesi olur.

Örneğin kırmızı başarı olursa, p = 1/3 ile 5 tane bernoulli denemesi mevcut denilir.

Bernoulli olasılık yoğunluk fonksiyonu:

Bir bernoulli denemesiyle ilgili X ragele değişkeninin olasılık yoğunluk fonksiyonu:

olarak hesaplanabilir. Burada p başarı, (1-p) başarısızlık olur.

Bernoulli beklendik değeri:

Bernoulli varyans hesabı:

olarak hesaplanabilr.

Binom rasgele değişkeni:

Bernoulli denemelir dizisinde başarılı sunuçlarının sayısı Y olsun. Deney n kere tekrarlanıyorsa olarak hesaplanabilir buna kartezyen uzay da denilir.

N denemedeki k başarının oluşma sayısı

bu yolların her birinin olasıllığını yazarsak:

denkleminde, (1-p) başarısızlık oranı n-k ise başarısızlık sayısını verir.

P{y=k}

burada Y , binom rasgele değişkeni olur.

Binom dağalımı olasılık yoğunluk fonksiyonu :

olarak hesaplanır.

b(n,p) = binom dağalımını gösterir, n ve p dağalımın parametreleridir ve n deney sayısını p ise başarının ihtimalini verir.

Örneğin, Y'nin b(12,1/4) olduğu bir dağalımda 12 deneme yapılırsa ¼ oranında başarı vardır deniilir, 12 denemeden 3'ü başarılı olur denilemez.

Örnek:

bir kutudan çekilen, 10 civcivden 6 dişi bulma olasılığı nedir?

P(dişi) = 0.5 olduğu a priori, (önceki bilgi) olarak biliniyor. Buna göre:

olarak yazılabilir. Dikkat edilirse, eşitliğin ilk tarafında olaslık dağalım fonksiyonu hesaplanmış ve 6 civciv çekilme ve 0.5 olasılığında hesaplanmıştır. Buna göre eşitliğin ilk tarafının sayısal değeri: 210 (dizilim olaslığı) x 0.015615 (dişi gelme olasılığı) x 0.0625 (erkek geleme olasılığı) = 0.2051 olarak hesaplanır.

Eşitliğin ikinci kısmı ise toplamsal olaslık dağalım fonksiyonu (cumulative probability function) hesabı yapılmıştır. Eşitliğin ikinci kısmının hesabında binom dağalımı tablosundan hesap yapılabilir buna göre p(x<=6) değeri tablodan 0.8281 ve p(x<=5) değeri 0.6230 olarak okunur ve yukarıdaki denklemin değeri 0.2051 olarak hesaplanır.

En az 6 civciv'in dişi olma olasılığı sorulmuş olsaydı cumulative probability distribution function formülünden:

Yukarıdaki ilk toplamsal kısım eşitliğin 2. kısmında görülen değer olarak da yazılabilir, ister ilk eşitlikten hesaplanarak ister ikinci eşitlikten tablo değerinden hesap yapılabilir.

Excepted value (beklenen değer) aynı zamanda ortalama değeridir.

Standart sapma değeri:

Örneğin, 2 değerli bir deneyin standart sapma değeri:şeklinde yazılabilir. O halde genel hali:

olarak yazılabilir

dağılımın grafiği aşağıdaki şekilde çizilebilir

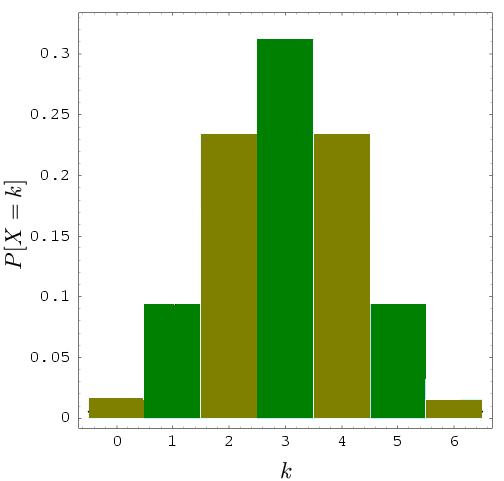
Örnek:

Uzun zaman yapılan gözlem sonucunda 10 parçanın 1'inin bozuk olduğu görülmüş. 5 parça seçilmiş, bozukların sayısı y olsun y = b(5,01) olarak gösterilebilir.

E(y) = np = 5(0.1) = 0.5 olur

olarak hesaplanır.

Şayet, en az 1 bozuk olma ihtimali sorulsaydı:

olarak hesaplanır (toplamın ilk kısmı p(y=0) ve ikinci kısmı p(y=1) ihtimallerini toplamıdır)

Geometrik binom dağılımı (Geometric Binomial Distribution):

Bernoulli denemelerinin sayısını önceden sabit tutmayıp r tane başarı oluşana kadar devam dersek bu dağılımlara geometrik dağılım denilir. Bu dağılımda x , yani ilgilenilen rasgele değişken, başarı elde edilmesinden önceki başarısılıkların sayısıdır.

Örneğin F,F,F,S sonuçları elde edilmiş olsun, ve başarı S, başarısızlıklar ise F ile gösterilsin. X= 3 olmuş olur ve olarak hesaplanabilir.

Geometrik binom dağılımının olasılık yoğunluk fonksiyonu:

f(x) = durumunda X'in geometrik dağılıma sahip olduğu söylenir.

benzer şekilde

o halde Y= X+1 olarak kabul edilirse:

Örnek

Biyoloji öğrencileri meve kurtları üzerinde deney yapıyorlar ve ¼ olasılıkla beyz, ¾ olasılıkla kırmızı gözlü olduklarını buluyorlar.

Rasgele alınan 1 beyaz kurttan önce, 3 kırmızı kurt gelme olasılığı nedir?

Olarak hesaplanır.

1 beyaz gözlü'den önce en çok 4 kurdun gözlenmesi ihtimali sorulsaydı

Y= X+1 için

Geometrik dağılımda E(X)= q/p ve

Y= X+1 için E(Y) = 1/p = 3 olarak hesaplanabilir.

Örnek :

n tamasının rasgele sıralanması tekrarsız olarak isteniyor. Zar atma olayı için bu durumu sağlayan kaç atış yapılmalıdır?

Soruyu daha iyi anlamak için n=6 ve ilk atış rasgele ilk sonucu verir. 2. sonuç için 6 olası sonuçtan sadece 5'i kalmıştır.

Benzer şekilde k-1 pozisyon doduktan sonra k. pozisyon için adayların sayısı n-k+1 'dir.

Olmuş olur.

O halde zar için gerekli atışların sayısı

beklenen atış sayısı ise 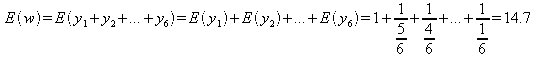dikkat edilirse, Beklenen değer hesaplanırken, toplam işlemi, beklenen değerlerin toplamıdır. Bu dönüşümden, eşitliklerden 3. denklem elde edilebilir. Eşitliklerden 4. sayısal değer ise her seferinde olasılığın 1 azalmasından dolayı paydanın küçülmesi şeklinde açıklanabilir.

Negatif binom dağılımı (Negative Binomial Distribution):

Şimdi dağılımın genel tanımına geri dönüp, r başarılı deneme durumuna bakalım (şimdiye kadar hep ilk başarı durumu incelenmiştir.)

bu durumda toplam atış sayısı x+r (başarılı ve başarısız atışların toplamı) olacaktır.

r. başarılı duruma kadar olan ihtimal hesabı:

olarak yazılabilir.Eşitliğin ilk kısmı r. başarıya kadar olan denemelerin dizilimini kombinasyonla hesaplarken ikinci kısım başarısızlıkların dizilimini olasılıkla hesaplar ve kombinasyonun tanımından bu iki sayının biribirine eşit olduğu hatırlanabilir.

r. başarının ihtimali p olarak tanımdan gelmektedir. Bu durumda r. başarı ihtimali iki denklemin çarpımı olarak hesaplanır:

bu değer, r. başarının (negatif binom dağılımının) olasılık yoğunluk fonksiyonudur.

Bu dağılıma Pólya veya Pascal dağılımı isimleri de verilir. Negatif denilmesinin sebebi n denemedeki başarısızlıkların sayısını vermesidir. Ve kesin olarak hesaplanamaz, yaklaşık değerdir:

Negatif binom dağılımının beklenen değeri:

bu durumda her bir değer için

Negatif binom dağılımının standart sapma değeri:

bu değer:

olur

Örnek:

meyva kurtlarını hatırlayacak olursak (¼ oranında beyaz kurt oluyordu) 3. beyazdan önce 10 tane kırmızı gözlü kurt olasılığı nedir?

Başarısız sayısı 10 ve başarılı sayısı 2 olması isteniyor. Formülden değeri aşağıdaki şekilde hesaplanır:

olarak hesaplanır.

Soruda 3. beyaz gözlüyü gözleyene kadar en fazla 12 kurt kontrol edilme olasılığı sorulsaydı

Örnek :

Bir makinanın bozuk parça üretme olasılığı 0.01 , her parça üretildikten sonra kontrol ediliyor. 1 tane bozuk parça için en az 100 parçanın kontrol edilmesi olasılığı nedir?

Olarak bulunur.

Poisson Dağılımı:

X, rasgele değişkeni için E[x] beklendik değeri dir

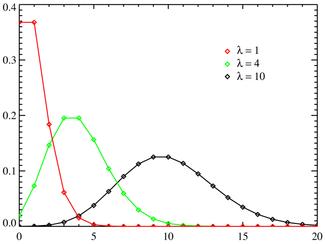
Yukarıdaki şekilde poisson dağalımının grafiği verilmiştir.

Örnek olarak X, = 5 ortalama değeri ile poison dağalımına sahip ise P(X=3) değerini hesaplayalım.

Örnek 3 dakikada 2 çağrı gelen bir çağrı merkezinde 9 dakikada 5 veya daha fazla çağrı yapılma olasılığı nedir?

Binom değerinin Poisson ile hesaplanması

Poison ile Binom dağalımındaki yaklaşık değerler de hesaplabilir bunun için poisson dağalımında olasılık değeri yerine değerini koyarak hesaplayalım:

bu alternatif çözüm, n>100 ve np < 10 gibi sayılar için oldukça başarılı çalışırken, düşük olasılık değerlerinde kötü sonuçlar vermektedir.

Örnek Bir lamba üreticisi, ürettiği lambaların %2'sinin bozuk olduğunu biliyor, bu lambalardan 100 tane bulunan bir kutuda en fazla 3 tane bozuk lamba bulunma olasılığı nedir?

Bu soruyu binom veya poisson dağalımı kullanarak çözebiliriz. Binom dağalımı ile:

aynı soruyu Poisson ile çözersek:

bulunur, dikkat edilirse iki yöntemin sonuçları oldukça yakındır.

Dağılımların Momenti

Ham moment = mesafe x büyüklük

İstatistikte ise rasgele bir değişkenin kuvvetinin ortalama değeridir. P(x) dağılımının n. momenti = Mn' olarak gösterilir.

Merkezi moment Ortalama değere uzaklığın momentidir.

Moment denklemi kullanılarak bir dağılımın beklendik değeri aşağıdaki şekilde hesaplanabilir:

bu hesaba bakmadan önce olduğunu hatırlayalım.

Merkezi moment formülündenolarak hesaplanabilir.

Ham moment formülünden

merkezi moment formülü, ham moment formülüyle yeniden düzenlenirse

olarak yazılabilir.

Mutlak moment

Genellenmiş moment

Moment Oluşturma Fonksiyonu

X'in diğer momentlerini hesaplamak için t gibi bir reel değişken ve bir reeel değişkenin fonksiyonu tanımlanır.

X, R uzayıyla tanımla ayrık tip rasgele değişken ve -h < t <h ve h>0 koşullarını sağlayan böyle bir fonksiyon bulunabiliyorsa, moment oluşma fonksiyonu oluştu diyebiliriz.

Türevin limit teoremindeki tanımını hatırlayacak olursak

,dir.

M(t)'nin oluşması t=0'da M(t)'nin türevlerinin de oluşması demektir.

yukarıdaki eşitliklerde t=0 için aşağıdaki beklendik değerlere ulaşılabilir:

O halde moment oluşma fonksinyonunu bulabilirsek momentin oluşması kolaylaşıyor.

Çıkarım yapılırsa:

Örnek: .X rasgele değişkeni için, , x = 1,2,3...olarak verilsin

moment oluşturma fonksiyonunu kullanırsak:

olarak yazılabilir.Eşitliğin ikinci kısmı geometrik seridir. Geometrik serileri hatırlayacak olursak:

olarak açılabilir. Şimdi moment fonksiyonumuzu geometrik seri olarak açalım:

serinin dönüşümü için

denkleminde, moment oluşturma fonksiyonundan hatırlanacağı üzere h oluşmuş oluyor.

Türev alınacak olursaolur ve sonuçta

Örnek x, rasgele değişkeni b(n,p) ile binom dağılımına sahip olsun, bu dağalımın beklendik değerini ve ortalama değerini moment fonksiyonu ile bulalım:

binom dağılımının fonksiyonunu hatırlarsak: 'dir.

denklemi açılımı şeklinde düşünülürse

şeklinde yazılabilir.

Şeklinde moment fonksiyonunun türevi alınırsa

olarak ortalama değeri bulunmuş olur.

Beklendik değer için ikinci türevin alınması gerekir:

olarak bulunur.

Örnek Bernoulli dağılımı için beklendik ve ortalama değerleri hesaplayalım.

olarak bulunur.

Moment fonksiyonunun en önemli özelliği, dağılımı tayin etmesidir. X[b1,b2,...] ile f(x) olası yoğunluk fonksiyonuna sahipse

Örnek: aşağıda verilen moment fonksiyonuna sahip dağılımın beklendik değer ve standart sapma değerlerini bulunuz.

çözüm için, Mc Laurin serisi yardımı ile aşağıdaki açılımlar her terim için ayrı ayrı yazılabilir:

yukarıdaki terimler taraf tarafa toplanırsa

olarak bulunur, burada r. terimin katsayısı:

olarak formülüze edilebilir. Dolayısıyla beklendik değer:

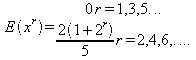olur bu durumda

olarak bulunur.

Ayrık Tip çok Değişkenli Dağılımlar

X,Y bir ayrık olasılık uzayında tanımlı iki fonksiyon olsun (R iki boyutlu bir uzay)

P(X=x,Y=y) olasılığı f(x,y) ile gösterilir ve X ve Y'nin birleşik olasılık yoğunluk fonksiyonu (Joint Probability Dense Function) olarak adlandırılır.

f(x,y)'nin sahip olması gereken özellikler:

1. 0<= f(x,y) <= 1

2. 

3. 

Örnek:

Bir zar 2 defa atılıyor. 36 olası sonuç var her ikili için x, küçük y ise büyük zarı göstersin.

x<=y ise, f(x,y) yani x ve y'nin birleşik olasılık yoğunluk fonksiyonu nedir?

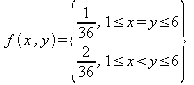Olarak bulunur.

Yukarıdaki denklemin de çıkartıldığı, olasılıkların grafikte gösterilmesi aşağıdaki şekilde olabilir:

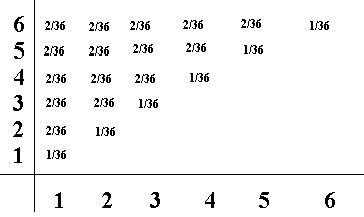
yukarıdaki şekilde iki zarın atıldığında gerçekleşebilecek ihtimaller gösteirlmiştir. Buna göre (1,2) gelme ihtimali 1/36'dır çünkü ilk zarın 2 veya ikinci zarın 2 gelme ihtimali vardır. Buna karşılık, (1,1) ikilisinin gelme ihtimali tektir. Bu da yukarıdaki birleşik olasılık yoğunluk fonksiyonunun nasıl bulunduğunu gösterir.

Aynı grafikte satır ve sütün toplamları alınacak olursa, aşağıdaki sayılar elde edilir.

Yukarıda da görüldüğü üzere, satır ve sütünların sayısal değerleri toplanarak kenarlarına yazılmıştır. Bu toplam değerlerine Marjinal olasılıklar denilir (kenar kelimesi margin'den geliyor) dolayısıyla örneğin 1. sütün için olan 11/36 toplamı, x değeri 1 ile sabitlendikten sonra y'nin alabileceği 1,2,3,4,5 ve 6 değerleri için elde edilecek olasılıkların toplamını gösterir.

Olarak ifade edilebilir ve bu bütün x değerleri için birleşik yoğunluk fonksiyonunun alabileceği değerlerdir.

Bağımlılık (Dependence):

X, ile Y'nin bağımlı değişken olup olmadığı aşağıdaki şekilde kontrol edilir:

Yukarıdaki zar örneğine geri dönülecek olursa, f(x=1,y=2) = P (x=1,y=2) = f(x=1)f(y=2) olur ve eşitliğin sol tarafında birleşik olasılık yoğunluk fonksiyonunun değeri 2/36 iken, eşitliğin sağ tarafındaki çarpımın değeri 1/6 x 1/6 'dan 1/26 olarak bulunur, bu durumda bu değişkenlerin bağımlı oldukları söylenebilir. Gerçekten de aralarında x<=y gibi bir bağ bulunması eşitliği bu hale sokmuştur.

Örnek:

X ve Y'nin birşelik olasılık yoğunluk fonksiyonu tanımlanıyor.

Buna göre olasılık yoğunluk fonksiyonu hesaplanırsa 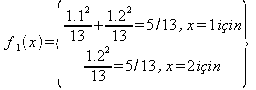olarak hesaplanır.

Bağımlılıkları test edilirse,

Şayet eşit çıksalardı, farklı oldukları bir örneğin olup olmadığı aranacaktı, bütün ihtimaller denendikten sonra, hiçbir ihtimal için eşitlik bozulmasaydı, bağımsız değişken, en az bir örnek için eşitlik bozulursa, bağımlı değişken olarak ifade edilirler.

İkiden fazla değişken için ve iki değişken için yazılan birleşik olasılık yoğunluk fonksiyonunu sağlar. Buna göre fonksiyon olur ve burada k boyutlu bir uzaydan bahsedildiği unutulmamalıdır.

Bağımsızlık testi de benzer şekilde ayrı ayrı çarpımlardan bulunur.

Örnek:

Bir dersi alan 200 öğrenci olsun bu öğrencilerin notları aşağıdaki şekilde dağıtılmış ise:

x1= 40 kişi => A

x2= 60 kişi => B

x3= 70 kişi => C

x4= 20 kişi => D

x5= 10 kişi => F

rasgele 25 kişillik bir örnek alıyoruz, her bir olası örneğin olasılığı nedir (kaç değişik şekilde 25 kişi seçilebilir)?

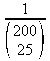Farklı seçme olasılığımız vardır.

Olarak yazılabilir.

O halde olasılık yoğunluk fonksiyonunu hesaplarsak 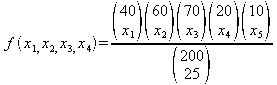olarak yazılabilir ve burada x5 için bulunan eşitlik yerine konulursa 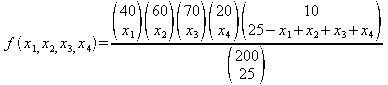olarak bulunabilir.

Örnek olarak 'ün marjinal yoğunluk fonksiyonunu hesaplayalım

olarak hesaplanır. Şimdi iki değişkenin marjinal olasılık yoğunluk fonksiyonunu hesaplarsak:

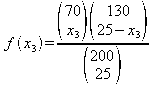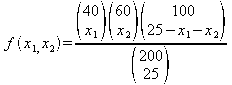olarak hesaplanır.

Hiper geometrik dağılımlar (hyper geometric distributions):

yukarıda verilen tek değişkenin marjinal yoğunluk fonksiyonu aslında bir hiper geometrik dağılımdır. Ve bu değeri veren marjinal yoğunluk fonksiyonuna hiper geometrik olasılık yoğunluk fonksiyonu denir. Bağımsızlığın testi için, aynı kurallar geçerlidir.

Örnek

x ve y'nin bağımsız olasılık yoğunluk fonksiyonu olarak verilmiş olsun. Aşağıdaki denemeleri yapalım:

a) X'in marjinal olasılık yoğunluk fonksiyonunu bulalım:

bu eşitlikteki X=1 ve X=2 değerlerini ayrı ayrı hesaplarsak:

olarak bulunur ve toplam 1'e eşittir. Yukarıdaki denemeden, olasılık yoğunluk fonksiyonu için genel bir gösterim çıkarmak istersek:

olarak bulunur.

b) Y'nin marjinal olasılık yoğunluk fonksiyonu hesaplanacak olursa:

bulunur ve benzer şekilde y için bir modellemeye gidilirse

bulunur

c) P(x>y) olasılığına bakallım. Sadece x=2 ve y=1 için mümkündür o halde P(X=2,Y=1) olmuş olur. Denklemde yerine konulursa

d) P(y=2x) = P(x=1, y=2) + P (x=2,y=4) = 3/32 + 6/32 = 9/32 olarak bulunur

e) P(x+y=3) için x=1 ve y=2 veya x=2 ve y=1 ihtimalleri olabilir. Buna göre P(x=1,y=2) + P (x=2,y=1) = 3/32 + 3/32 = 6/32 bulunur.

f) P(x<= 3-y) için x=1 ve y=1 (2/32) veya x=1 ve y=2 (3/32) veya x=2 ve y=1 (3/32) bulunur bunların toplamı ise 8/32 yapar.

g) x ve y bağımsız mıdır?

f(x,y)= f(x)f(y) eşitliği test edilir buna göre

eşitliği kontrol edilir ve eşit olmadığı için bağımlı oldukları gösterilmiş olur.

Kovaryans (Covariance) ve Korelasyon (Correlation)

Kovaryans ve Korelasyon için en az iki değişken gereklidir. Buna göre aşağıdaki girişten sonra bu terimleri tanımlayalım.

x1,x2,...xn ayrık tipte birleşik olasılık yoğunluk fonksiyonuna sahip rasgele değişkenlerimiz olsun. f(x1,x2,...xn) için u(x1,x2,...xn) ayrık tipte rasgele değişkenlerin bir fonksiyonu olsun. Ve bu fonksiyonun beklendik değerini yazmaya çalışalım.

Örnek:

Bir kutuda 8 tane top var. Bunlardan

3 tanesinin üzerinde (0,0)

2 tanesinin üzerinde (0,1)

2 tanesinin üzerinde (1,0)

1 tanesinin üzerinde (1,1) sayıları yazıyor. Bir oyuncu bu toplardan birisini seçiyor ve seçtiği topun üzerinde yazan sayıların toplamı kadar para kazanıyor. Buna göre oyuncunun oyun için ne kadar para vermesi beklenir?

1. koordinat X1 ile ve 2. koordinat olsun buna göre

olarak hesaplanabilir. Şayet birleşik olasılık yoğunluk fonksiyonunu hesaplayacak olursak olarak hesaplanır. Beklendik değer ise u fonksiyonunu kullanarak aşağıdaki şekilde hesaplanabilir:

olur.

Bu birden fazla değişkene sahip u fonksiyonu için Ortalama değer, Varyans , Kovaryans ve Korelasyon değerlerini formülize edelim:

Ortalama Değer

olsun. Beklendik değeri aşağıdaki şekilde hesaplanabilir:

olur.

Varyans:

olarak bulunur.

Kovaryans (Covariance):

olarak adlandırılır. Ve olarak gösterilir. Bu değer, iki değişkenin ortalamalarına göre birlikte ne kadar değiştiklerini gösterir. Olarak çarpımı dağıtabiliriz. Olduğu hatırlanırsa kovaryans değeri olarak yazılabilir.

Kovaryans, pozitifse değişkenlerden ikisi de ortalamnın aynı yönünde yer alıyor demektir (ikisi de eksi veya ikisi de artı). Şayet kovaryans, eksi değer alıyorsa, değişkenler farklı yönlerde demektir. Eğer iki değişken bağımsızsa kovaryansları 0'dır. Ispatı şu şekilde yapılabilir:

koşulu sağlanıyorsa bağımsızdırlar.

Korelasyon Katsayısı (Correlation Coefficient)

Eğer standart sapmaları pozitif ise olacaktır daha önceki notlara bakılırsa olduğu hatırlanır. Bu bilgiler ışığında bu eşitlik yeniden düzenlenirse olarak da yazılabilir.

Burada korelasyon katsayısı için olmalıdır ve – değerler için kovaryansa benzer şekilde ters yön, + değerler için ise kovaryansa benzer şekilde aynı yön olduklarını çıkarabiliriz. Kovaryansa benzer şekilde bağımsız değişkenler için korelasyon 0 çıkar ancak değeri 0 çıkarsa bağımsız değişkenlerdir diyemeyiz (linear olarak bağımsızdırlar diyebiliriz) örneğin için korrelasyon değeri 0 çıkar ama bağımlı değişkenlerdir.

Dolayısıyla, korolasyon birbirlerine bağlılıklarını , Kovariance ise ortalama değerlerin ne kadar saptığını gösterir.

Korelasyon kullanarak beklendik değer hesaplanması:

olduğunu hatırlayalım, şimdi covaryans bilgisinin beklendik değer cinsinden yazalım. Olarak yazılabilir.

Koşullu Dağalımlar (Conditional Distributions)

g fonksiyonuna sahip bir ayrık (discrete) X olduğunu düşünelim. Bu durumda S (Örnek Uzay ( Sample Space)) sayılabilirdir ve g(x) > 0 olduğunu düşünebiliriz. Bu durumda

olacağını daha önce görmüştük. Şimdi bu durumun koşullu olasılık yoğunluk fonksiyonunu görelim (conditional probability density function)

T kümesinde değerler alan Y gibi bir rasgele değişkenin olduğunu düşünelim. Bu durumda (X,Y) değişken ikilisi, SxT çarpımı içinde değerler almaktadır. (X,Y)'nin bileşik olasılık yoğunluk fonksiyonunun (joint probability density function) f olduğunu düşünelim. Bu durumda koşullu olasılık yoğunluk fonksiyonu:

olarak yazılabilir.

X=x durumu verildiğinde, Y'nin koşullu olasılık yoğunluk fonksiyonu, aşağıdaki şekilde hesaplanabilir:

olarka gösterilebilir.

Koşullu dağalımların bağımsızlığı (Independence of Conditional Distribution)

X ve Y değişkenleri aşağıdaki iki koşul için de bağımsızdır denilebilir.

Örnek:

İki adil zar'ın atıldığını ve (X1,X2) sonuçları alındığını kabul edelim. Buna göre U = min {X1,X2} ve V= max {X1,X2} olsun.

a. U verilmişken V=v için koşullu yoğunluğunu hesaplayınız

b. V verilmişken U=u için koşullu yoğunluğunu hesaplayınız

Cevap:

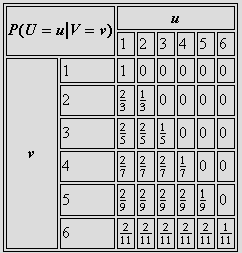
Aynı sorunun bir de para atarak yapıldığını düşünelim. N, zar sonucunu Y ise para sonucunu tutsun, buna göre :

a. (N,Y) için birleşik yoğunluğu bulunuz.

b. Y'nin yoğunluğunu bulunuz.

c. N'in Y=k için yoğunluğunu bulunuz

Çözüm:

a ve b şıklarının çözümü ilk tabloda, c şıkkının çözümü ikinci tabloda gösteirlmiştir.

Koşullu Beklendik Değerler (Conditional Expected Value)

X=x verilmişse Y'nin koşullu ortalama değeri:

olur.

Koşullu varyans (Conditional Variance)

X=x verildiğinde Y'nin koşullu varyansı

Sürekli tip rasgele değişkenler

Uzayları, aralıklar veya aralıkların birleşimleri olan rasgele değişkenler sürekli tip olarak adlandırılır.

h(x) bağıl frekans histogramı olsun (sürekli tip değişkenin n defa gözlenmesi ile ilgili )

olasılığının biçilmiş değerini verir. Bu olasılık, x'in a ile b arasında olma olasılığıdır.

n sınırsız arttırırlırsa, (yeterince büyük olduğunda) h(x), f(x)'e (olasılık yoğunluk fonksiyonuna) yaklaşır.

Bu olasılığın grafiksel gösterimi aşağıda çizilmiştir:

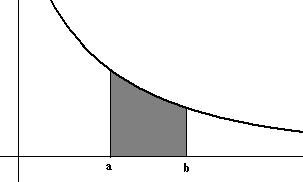
n, sonsuza yaklaşırken, f(x) ile x arasında kalan alan 1'e eşittir.

f(x) sürekli tip x rasgele değişkeninin olasılık yoğunluk fonksiyonu şu özelliklere sahiptir:

• f(x) > o

• 

• 

Örnek:

R= { X: 0<x<inf} uzayı ile X rasgele değişkeni bir elektron tüpünün ömrü olsun. Diye verilmiş, ve

Buan göre Elektron tüpünün ömrünün 100 saatten fazla olma olasılığı nedir?

Sürekli tip değişkenlerde dağalım fonksiyonu (Cumulative distribution function)

olur.

P(x=a)=0 , bütün reel a değerleri için.

P(a<x<b) = P(x<b) – P(x<a)

Ayrık tip değişkenlerde f(x)= P(X=x) sınırıdır.

Sürekli tip değişkenlerde f(x) sınırlı olmak zorunda değildir. f(x), sürekli olmak zorunda da değildir.

Örnek fonksiyonlar aşağıda gösterilmiştir. Olasılık yoğunluk fonksiyonu aşağıdaki şekilde olabilir:

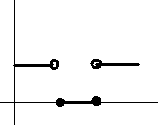
Bu olasılık yoğunluk fonksiyonunun cumulative dağılım fonksiyonu aşağıdaki şekildedir:

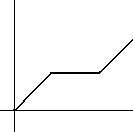
Dikkat edilirse, ilk grafik, ikinci grafiğin türevidir.

Matematiksel Beklendik Değer:

X'in beklnedik veya ortalama değeri

X'in varyansı

standart sapması da olarak hesaplanır.

Eğer oluşursa moment türetme fonksiyonu

Uniform Dağalımlar (Uniform Distributions)

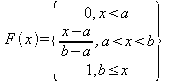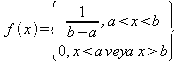x, [a,b] ve aralığından rasgele seçilen bir değişkeni göstersin. Bu aralıktan seçilen noktanın olasılığı aralığın uzunluğuyla orantılıdır. Ve olarak verilmektedir. X'in dağalım fonksiyonu olarak hesaplanabilir ve olasılık yoğunluk fonksiyonu olarak yazılabilir .Bu fonksiyonların grafiği aşağıdaki şekildedir.

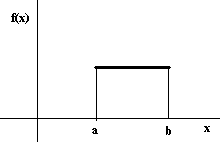
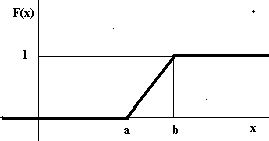
Yine dikkat edilirse, ikinci grafiğin türevi ilk grafiktir.

Yukarıda tanımı yapılan dağalım, uniform dağalımdır ve U(a,b) şeklinde gösterilir.

Bu döküman, Yrd. Doç. Dr. SIRMA YAVUZ'un derslerinden esinlenerek hazırlanmıştır, web sitesi