Özet
Bu yazının amacı, Dinamik Markov Coding kullanılarak sıkıştırma yöntemini incelemektir. Bu yazı, “Data Compression Using Dynamic Markov Modelling” ve G. V. CORMACK AND R. N. S. HORSPOOL tarafından yazılmış olan makalenin incelenmesini içermektedir
Dynamic Markov Coding yeni bir sıkıştırma algoritması olmayıp, mevcut sıkıştırma algoritmalarının üzerine getirilen yeni bir yaklaşımdır. Yaklaşım binary kodlama üzerine kurulu olup, u yaklaşımda başarı veri sıkıştırması sırasında gelen .bitlerin tahminine ve değerlendirmesine dayanmaktadır. Markov chain modelinin oluşturulması ve bu modelin kendisini her gelen yeni bite gore güncellemesi bu çalışmanın temelini oluşturmaktadır. Ayrıca Dinamik Markov Coding için arithmetic coding yöntemlerinden birisi olan gauzzo yöntemi de bu çalışmada incelenmiştir.
1. Giriş
Bilindiği üzere günümüzde oldukça fazla sayıda sıkıştırma algoritması bulunmaktadır. Bu algoritmaların daha verimli çalışması için yapılan çeşitli çalışmalardan birisi de istatistiksel bir modele dayanan Makrov Kodlamasıdır. İlk olarak rus matematikçi Andrey Markov tarafından geliştirilen bu yöntem stochastic process üzerine kurulmuştur. Bu yazıda stochastic process ve markov chain konularına giriş yaptıktan sonra markov coding ile verinin ifadesine ve bu ifade biçiminin nasıl dinamik olabileceği incelenecektir. Son olarak bu ifade biçiminin gauzzo yöntemi ile sıkıştırılması anlatılacaktır. .
2. Stochastic Processlere Giriş
Stochastic Process, olasılık uzayı (Ω, S, Pr) üzerinde tanımlı random variable X ‘lerin sekansıdır. Öyleki her X için bir I → D fonksiyonu tanımlıdır.
Bu modelde I → D bağlantısındaki D, codomain uzayını ve I codomainde tanımlı fonksiyonları ifade etmektedir.
(Ω, S, Pr) sisteminde Pr. Olasılık değerleri, S fonksiyonlar kümesini ve Ω ihtimaller kümesini göstermektedir. Yani P (Ω )=1 olmalıdır.
Stochastic process discrete veya continous olabilir.
Örneğin discerete time için random variableların alabileceği değerler, {0, 1, 2, 3, ...}. olurken continous time için bir fonksiyon ya da zaman parametresi olabilir
3. Markov Chain Modele Giriş
Bir stochastic process örneği olan markov chain model aşağıdaki şekilde modellenmektedir:
![]()
Stochastic model hatırlanacak olursa, Pr modeli random variable Xlerin her zaman aralığı için ifadesinden oluşmaktadır.
Daha basit anlaşılması için aşağıdaki örneği inceleyelim
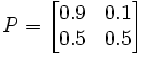
Örneğin yukarıdaki matrixte markov özelliği taşıyan bir matrix alınmıştır. Bu matrix hava durumunu gösteren bilgileri içermektedir ve ilk satır yağmurlu olma olasılığını, ikinci satır ise güneşli olma olasılığını göstermektedir. Dolayısıyla yağmurlu olma olasılığı %90 iken olmama olasılığı %10 benzer şekilde güneşli olma olasılığı %50 iken olmama olasılığı %50 olarak verilmiştir.
Şimdi bu matrix kullanılarak hava durumu tahmini yapılması durumunda, bugünkü hava durumu bilgisi gerekmektedir. Diyelim ki bugün hava yağmurlu ve yarının hava tahminini istiyoruz. Durumun formülasyonu aşağıdaki şekilde olacaktır.
![]()
Yukarıdaki örnekte görüldüğü üzere tahmin matriximiz, [1 0] matrixi ile çarpılmıştır. Burada [1 0] matrixinin gösterdiği değer, 1 yağmurlu olma durumu ve 0 olmama durumunu ifade etmektedir.
Şayet bugün yağmurluysa, matrix [1 0] şeklinde olmalıdır (gerçekleşmiş ihtimal)
Dolayısıyla stochastic moelimizin içinci değişkenini elde etmiş oluyoruz. Bu durumda (yani yağmurlu bir günün ardından yukarıdaki matrix ile yeni günün hesaplnamasında) %90 yağmurlu ve %10 yağmursuz bir gün ihtimali elde edilmiş olur.
İkinci günün de yağmurlu olma olasılığını istiyorsak modelimizi aşağıdaki şekilde ilerletmemiz gerekir:
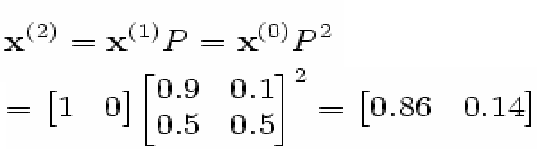
görüldüğü üzere, matriximizin kendis ile çarpımından elde edilen değeri mevcut günden elde edilen değerle çarparak 2. günün ihtimali elde edilmiş oluyor.
Yeni değerlerde %86 ihtimaliyle yağmurlu gün olurken %14 yağmursuz bir gün bekliyor demektir.
4. Veriyi Gösteren Markov Chain Model İnşası
Önceki bölümde giriş yapılan markov chain modelleri
![]()
Şeklindeki stochastic modellerdir. Bu modellerin her durum için bir sonraki durumdan gösterdikleri bir olasılık bulunmakta ve bu olasılıklar yönlendirilmiş (directed) graphlar ile gösterilebilmektedir. Markov chainlere en güzel örneklerden birisi de Sonlu durum makineleridir (FSM).
Bu çalışmada yapılan markov chain model, veriyi binary olarak 1 ve 0lar ile modellemektedir. Buna göre gerek yazı gerekse grafiksel verilerin binary kodlaması üzerinde markov chain uygulamak mümkündür. Aşağıdaki tabloda örnek veri gelme durumları incelenmiştir:
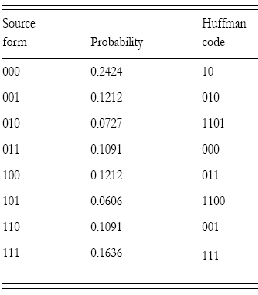
Yukarıdaki tabloda görüldüğü üzere, gelen sayıların binary olması durumunda 3 farklı sayının gelebileceği 8 ayrı ihtimal incelenmiştir. Bu ihtimallerin olasılık değerleri ortadaki kolonda verilmiş ve bu sayıların huffman kodu en son kolonda gösterilmiştir. Bilindiği üzere huffman kodu mümkün olan en az biti mümkün olan en çok tekrarlanmış veri için kullanmaya çalışmaktadır. Dolayısıyla en çok gelme olasılığı olan 000 yazısı için en az bit kullanılmıştır.
Şimdi yukarıdaki tablo için bir markov chain model üretilecek olursa:
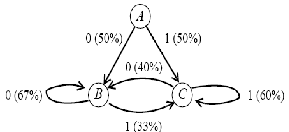
Yukarıdaki şekilde, 3 ayrı durum incelenmitir. Başlangıç A düğümünden yapılmaktadır.
Görüldüğü üzere A başlangıç durumunda ya 0 ya da 1 gelmekte ve olasılıkları eşit şekilde %50 olmaktadır. Ardından gelinen B ve C düğümlerinde yeni değerler ve olasılıkları şekil üzerinde gösterilmiştir.
5. Markov Chainin Dinamik zamanda oluşutrulması
Veri sıkıştırmasında, adaptive veya adaptive olmayan yöntemler kullanılabilmektedir. Dynamic Markov Coding, adaptive bir yöntem önermektedir. Buna göre verinin gelmesi durumuna göre markov modelimizi güncellememiz gerekmektedir.
Buna göre grafik boş iken başlanır ve aşağıdaki şekillerde veriler güncellenir:
Prob {sayı = 0 | bulunulan node = A} = n0 / (n0 + n1)
Prob {sayı = 1 | bulunulan node = A} = n1 / (n0 + n1)
Prob {sayı = 0 | bulunulan node = A}
= (n0 + c) / (n0 + n1 + 2c)
Prob {sayı = 1 | bulunulan node = A}
= (n1 + c) / (n0 + n1 + 2c)
buradaki n1: 1lerin sayısı, n2: 2lerin sayısı ve c, 0 dan büyük herhangi bir sabit sayıyı ifade etmektedir. Gelen 0 ve 1 lerin sayısı büyüdükçe, c değeri anlamını yitirmektedir.
Örnekte yukarıda verilen formülün kullanılması durumunda markov modeli için istatistiksel değerleri içeren kolların inşa edilmesi mümkün olmaktadır.
Grafik inşası sırasında karşılaşılan bir diğer sorun, grafiğin önceki değeri unutması ve bulunan bir duruma nereden geldiğinin anlaşılmasını engelleyen karmaşa ihtimalleridir. Bu durum aşağıdaki şekilde gösterilmiştir:
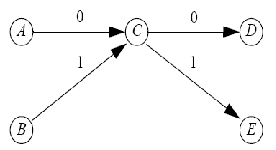
Yukarıdaki grafik, inşa edilmiş olan markov chain model içerisinde bir yada daha çok yerde görülebilen bir durumdur. Buna göre C durumundan D ve E durumlarına belirli (deterministic) bir şekilde gidilebilmektedir, yani C durumundayken 0 ve 1 gelme olasılıkları belirlenmiştir. Ayrıca C durumuna 0 veya 1 ile gelebileceğimizi bilmekteyiz. Ancak C durumuna 0 ile mi 1 ile mi gelindiği tam olarak bilinmemektedir.
Stochastic processler hatırlanacak olursa, bir sonraki durum önceki durumlara bağlı olmaktadır (hava durumunu hatırlayınız) dolayısıyla C durumuna hangi sayı ile gelindiği bilinmelidir. Bu durumda önerilen çözüm clonlama yöntemidir.
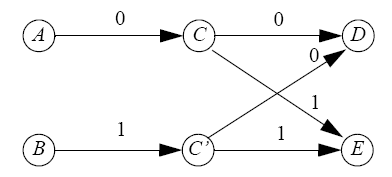
Yukarıdaki grafik, belirsiz C durumunun klonlanmış halini göstermektedir. Buna göre A durumundan C durumuna 0 ile gelinebilmekteyken artık B durumundan C durumuna gidiş bulunmamakta bunun yerine yeni klonlanmış olan C’ durumuna gidilebilmektedir. Dolayısıyla artık C durumuna geliniyorsa bunun 0 ile, C’ durumuna geliniyorsa bunun 1 ile olduğu bilinebilmektedir. Ve D durumuna gelinme ihtimali ancak 00 veya 10 olurken E durumu 01 veya 11 ihtimallerine cevap vermektedir.
Klonlama özelliği ilk başlarda oldukça faydalı görülmesine karşılık, zaman içerisinde hafıza sorunları ve kompleksliğin artması gibi sebeplerle durdurulmalıdır. Bu işlemin ne zaman durdurulacağı ise iki ihtimale bağlanmıştır bunlar:
Bir node kendisine mevcut noddan gitmek için kullanılan Transation sayısı eşik değeri aştığında ve
Mevcut noddan kendisine gitmek için kullanılan bütün Transitionların sayısı eşik değerini aştığında clonelanır
(bkz. Kirchoff Kanunu)
Bu modelde bir diğer problem ise başlangıçta kullanılacak olan markov chain modeldir. Bunun için önerilen boş bir grafik ile başlamak veya mevcut verinin en küçük yapıtaşını tutan bir grafik ile başlamaktır. Örneğin
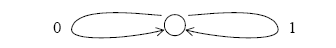
Yukarıdaki grafik 1 veya 0 ile dolaşılabilen tek bir düğüm içermektedir. Şayet veri modeli, 0 ve 1lerden oluşuyorsa kullanılabilecek en basit model yukarıdaki şekildedir.
Benzer şekilde ASCII kodlarından oluşan ve 256 sembolü gösteren bir veri modeli oluşturulacaksa bunun için 8 seviyeli bir düğüm yapısı kullanılabilir
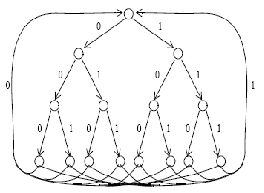
Yukarıdaki grafik, fiziksel sebeplerden dolayı 3 seviyeli bir ağacı göstermektedir. 8 seviyeli olan ağaç da benzer şekilde çizilebilir.
6. Sıkıştırma örneği
Yukarıdaki bölümlerde anlatılan modeller bir sıkıştırma metodolojisi olan dinamik markov modelin inşasını ve adaptasyonunu içermektedir. Bu model basit bir şekilde herhangi bir aritmetik sıkıştırma yöntemine uygulanabilir örnek model olarak gauzzo sıkıştırması ele alınacak olursa, sıkıştırma yönteminin karakteristiği aşağıdaki şekilde olacaktır:
Guazzo katsayılarının hesaplanmasında sayı düzeni bozulmadan ondalıklı sayıya çevrilir örneğin 01101 sayısı è 0.01101 olur ve oranı (13/16) olur.
Dolayısıyla sayı domaini 0 ile 0.11111… sayıları arası sayılardan oluşmaktadır. Ve bu sayılar arasında binary dallanma mümkündür örneğin ilk değerin 0 olmasına göre 0.011.. olurken 1 olmasına göre 0.111… olmaktadır
Bu yöntemde oranlara göre markov chain içinde hareket mümkün olup herhangi bir arithmetik kodlamada kullanılan alçak ve yüksek değerlere eşitlenebilmektedir.
7. Sonuç
Bu yazıda mevcut sıkıştırma yöntemlerine getirilen bir yenilik olarak dinamik markov chain kodlaması incelenmiştir başarı oranı aşağıdaki grafikte verilmiştir:
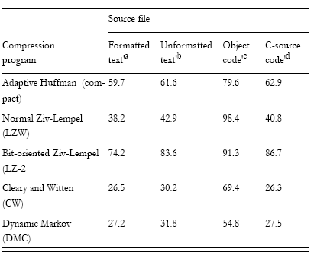
bu yöntem yeni bir sıkıştırma algoritması olmayıp mevcut algoritmalara (tercihen aritmetik kodlama) getirilmiş yeni bir yaklaşımdır. Ve verinin binary olarak tutulmasını ve veri akışına göre istatistiksel olarak modellenerek markov chain ile gösterilmesini önermektedir.
8. Referanslar
Vector Compaction Using Dynamic Markov Models
Radu Marculescu, Diana Marculescu, Massoud Pedram
Data Compression Using Dynamic Markov Modelling
G. V. CORMACK* AND R. N. S. HORSPOOL*
Using Markov Chains for Link Prediction in Adaptive Web Sites
Jianhan Zhu, Jun Hong, and John G. Hughes